题目内容
已知(x2-| 1 | ||
|
分析:先求出展开式中的常数项T,求得函数的周期是2,由于g(x)=f(x)-kx-k有4个零点,即函数f(x)与r(x)=kx+k有四个交点,根据两个函数的图象特征转化出等价条件,得到关于k的不等式,求解易得.
解答: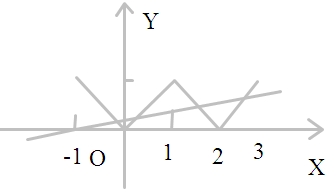 解:∵(x2-
解:∵(x2-
)5的常数项为
×
=2
∴f(x)是以2为周期的偶函数
∵区间[-1,3]是两个周期
∴区间[-1,3]内,函数g(x)=f(x)-kx-k有4个零点可转化为f(x)与r(x)=kx+k有四个交点
当k=0时,两函数图象只有两个交点,不合题意
当k≠0时,∵r(-1)=0,两函数图象有四个交点,必有0<r(3)≤1解得0<k≤
故答案为:(0,
]
 解:∵(x2-
解:∵(x2-| 1 | ||
|
| C | 2 5 |
| 1 |
| 5 |
∴f(x)是以2为周期的偶函数
∵区间[-1,3]是两个周期
∴区间[-1,3]内,函数g(x)=f(x)-kx-k有4个零点可转化为f(x)与r(x)=kx+k有四个交点
当k=0时,两函数图象只有两个交点,不合题意
当k≠0时,∵r(-1)=0,两函数图象有四个交点,必有0<r(3)≤1解得0<k≤
| 1 |
| 4 |
故答案为:(0,
| 1 |
| 4 |
点评:本题考点二项式定理,主要考查依据题设条件灵活转化的能力,如g(x)=f(x)-kx-k有4个零点,即函数f(x)与r(x)=kx+k有四个交点,灵活转化是正确转化是解题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目