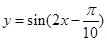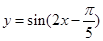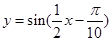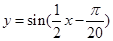题目内容
已知定义在R上的函数f(x)是周期为3的奇函数,当 时,
时, ,则函数f(x)在区间[0,5]上的零点个数为( )
,则函数f(x)在区间[0,5]上的零点个数为( )
| A.9 | B.8 | C.7 | D.6 |
B
解析试题分析:  周期为2,当
周期为2,当 时,函数图象与x轴有2个交点,因为函数f(x)是周期为3的奇函数,所以函数图象关于x轴对称,画出简图,可以发现在区间[0,5]上有8个零点.
时,函数图象与x轴有2个交点,因为函数f(x)是周期为3的奇函数,所以函数图象关于x轴对称,画出简图,可以发现在区间[0,5]上有8个零点.
考点:本小题主要考查函数的奇偶性、对称性和函数的零点个数问题。
点评:解决此类问题的关键是根据函数的性质将函数的简图画出来,将零点个数问题转化为函数图象与x轴的交点个数问题.

练习册系列答案
相关题目
函数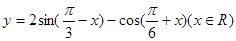 的最小值是( )
的最小值是( )
A. | B.-2 | C.-1 | D.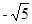 |
为了得到函数 的图象,只需将函数
的图象,只需将函数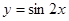 的图
的图
象( )
A.向左平移 个长度单位 个长度单位 | B.向右平移 个长度单位 个长度单位 |
C.向左平移 个长度单位 个长度单位 | D.向右平移 个长度单位 个长度单位 |
为得到函数 的图象,只需将函数
的图象,只需将函数 的图像( )
的图像( )
A.向左平移 个长度单位 个长度单位 | B.向右平移 个长度单位 个长度单位 |
C.向左平移 个长度单位 个长度单位 | D.向右平移 个长度单位 个长度单位 |
已知 ,则
,则 =( )
=( )
A. | B.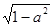 | C. | D.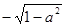 |
已知 ,函数f(x)=sin(
,函数f(x)=sin( x+
x+ )在(
)在( ,π)单调递减。则
,π)单调递减。则 的取值范围是
的取值范围是
A.[ , , ] ] | B.[ , , ] ] | C.(O, ] ] | D.(0,2] |
若 为锐角三角形
为锐角三角形 的两个内角,则点
的两个内角,则点
位于( )
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
已知 ,则
,则 =( )
=( )
A. | B. | C. | D. |
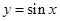 的图像上所有的点向右平行移动
的图像上所有的点向右平行移动 个单位长度,再把所得各点的横坐标伸长到原来的
个单位长度,再把所得各点的横坐标伸长到原来的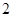 倍(纵坐标不变),所得图像的函数解析式是( )
倍(纵坐标不变),所得图像的函数解析式是( )