题目内容
设函数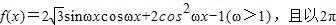 为最小正周期.
为最小正周期.(1)求f(x)的解析式,并求当
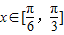 时,f(x)的取值范围;
时,f(x)的取值范围;(2)若
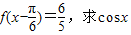 的值.
的值.
【答案】分析:(1)先根据二倍角公式对原函数进行化简整理,再结合周期为2π即可求出f(x)的解析式;再结合自变量的取值范围结合正弦函数的单调性即可求出f(x)的取值范围;
(2)先根据已知条件求出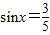 ,再结合同角三角函数之间的关系求出结论即可.
,再结合同角三角函数之间的关系求出结论即可.
解答:解:(1)∵ =
=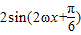 .…(2分)
.…(2分)
∵T=2π,∴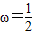 .
.
∴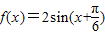 .…(4分)
.…(4分)
由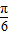 ≤x≤
≤x≤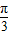 ,得
,得 ≤x+
≤x+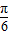 ≤
≤ ,
,
于是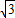 ≤f(x)≤2.
≤f(x)≤2.
即f (x)的取值范围为[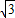 ,2]. …(8分)
,2]. …(8分)
(2)∵ ,
,
即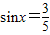 .…(10分)
.…(10分)
∴ . …(12分)
. …(12分)
点评:本题主要考查三角函数中的恒等变换.解决这一类型题目的关键在于对公式的熟练掌握以及灵活运用.
(2)先根据已知条件求出
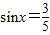 ,再结合同角三角函数之间的关系求出结论即可.
,再结合同角三角函数之间的关系求出结论即可.解答:解:(1)∵
 =
=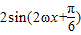 .…(2分)
.…(2分)∵T=2π,∴
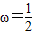 .
.∴
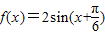 .…(4分)
.…(4分)由
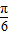 ≤x≤
≤x≤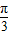 ,得
,得 ≤x+
≤x+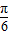 ≤
≤ ,
,于是
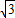 ≤f(x)≤2.
≤f(x)≤2.即f (x)的取值范围为[
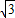 ,2]. …(8分)
,2]. …(8分)(2)∵
 ,
,即
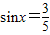 .…(10分)
.…(10分)∴
 . …(12分)
. …(12分)点评:本题主要考查三角函数中的恒等变换.解决这一类型题目的关键在于对公式的熟练掌握以及灵活运用.

练习册系列答案
相关题目
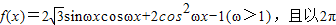 为最小正周期.
为最小正周期.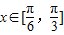 时,f(x)的取值范围;
时,f(x)的取值范围;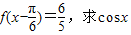 的值.
的值.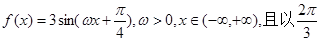 为最小正周期.
为最小正周期. 的解析式;
的解析式; 的值.
的值. 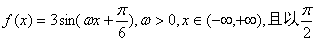 为最小正周期.
为最小正周期.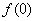 ;
;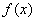 的解析式;
的解析式; 的值.
的值.