题目内容
平面直角坐标系中,圆O方程为x2+y2=1,直线y=2x与圆O交于A,B两点,又知角α、β的始边是x轴,终边分别为OA和OB,则cos(α+β)=分析:由题意可得 β=π+α,tanα=2,α 为锐角,可得 cosα 的值,故cos(α+β)=cos(π+2α)=-cos2α,由二倍角的余弦公式求得结果.
解答:解:由题意可得 β=π+α,tanα=2,α 为锐角,
∴cosα=
,sinα=
.
故cos(α+β)=cos(π+2α)=-cos2α=1-2cos2α=1-2×
=
,
故答案为
.
∴cosα=
| ||
| 5 |
2
| ||
| 5 |
故cos(α+β)=cos(π+2α)=-cos2α=1-2cos2α=1-2×
| 1 |
| 5 |
| 3 |
| 5 |
故答案为
| 3 |
| 5 |
点评:本题考查两角和的余弦公式,同角三角函数的基本关系,以及诱导公式、二倍角的余弦公式的应用,求出 cosα=
,是解题的关键.
| ||
| 5 |

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
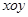 中,圆
中,圆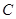 的方程为
的方程为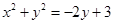 ,直线
,直线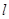 的方程为
的方程为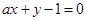 ,则直线
,则直线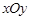 中,圆
中,圆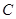 的方程为
的方程为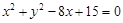 ,若直线
,若直线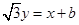 上至少存在一点,使得以该点为圆心,1为半径的圆与圆
上至少存在一点,使得以该点为圆心,1为半径的圆与圆 的最大值是 ;
的最大值是 ; 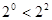 ,
,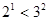 ,
,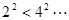 猜想
猜想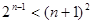 (
( )
)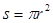 ,单位圆的面积
,单位圆的面积
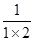 、
、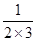 、
、 的通项为
的通项为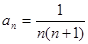 (
(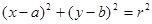 推测空间直角坐标系中球的方程为
推测空间直角坐标系中球的方程为