题目内容
(1)若角α的终边和函数y=-|x|的图象重合,试写出角α的集合;
(2)已知角α是第二象限角,试确定2α、![]() 所在的象限;
所在的象限;
(3)若θ角的终边与![]() 角的终边相同,求在[
角的终边相同,求在[![]() ,
,![]() ]内终边与
]内终边与![]() 角的终边相同的角.
角的终边相同的角.
答案:
解析:
解析:
|
思路 求终边相同的角的集合,方法是先求出[0,2π]之间符合条件的角,再根据周期性写出符合条件的角的集合. 解答 (1)由于y=-|x|的图象是三、四象限的平分线,故在 (2)∵α是第二象限角, ∴k· 2k· ∴故2α是第三、第四象限或角的终边在y轴负半轴上. ∵k· 当k=2m(m∈Z)时,m· 当k=2m+1(m∈Z)时,m· ∴ (3)θ=k· 依题意得0≤k· |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




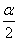 所在的象限;
所在的象限;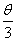 的终边相同的角.
的终边相同的角.