题目内容
已知向量 ,
, .且x
.且x
求(1)
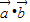 ;
;(2)若f(x)=
 -2λ|
-2λ| |的最小值是-
|的最小值是- ,求λ的值.
,求λ的值.
【答案】分析:(1)利用向量的数量积的运算,根据两向量的坐标求得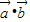 ,并利用二倍角的余弦化简整理.
,并利用二倍角的余弦化简整理.
(2)根据(1)和题设向量的坐标求得函数f(x)的解析式,利用二倍角的余弦化简整理,然后利用x的范围确定cosx的范围,看λ∈[0,1],λ>1和λ<-1时根据二次函数的性质可确定函数的最小值,求得λ.
解答:解:(1)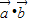 =
=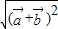 =
=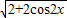 =2cosx(x∈[0,
=2cosx(x∈[0,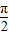 ])
])
(2)由(1)知:f(x)=cos2x-4λcosx=2cos2x-4λcosx-1=2(cosx-λ)2-2λ2-1
∵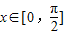
∴cosx∈[0,1],
当λ∈[0,1]时,f(x)min=-2λ2-1,而 ,
,
所以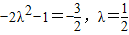 ,
,
当λ<0时,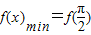 =2λ2-2λ2-1=-1,
=2λ2-2λ2-1=-1,
而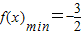 ,不符合题意.
,不符合题意.
当λ>1时,f(x)min=f(0)=2-4λ-1=-4λ+1,而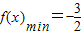
所以-4λ+1=-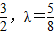 这与λ>1矛盾
这与λ>1矛盾
综上述λ的值为 .
.
点评:本题主要考查了三角函数的最值,平面向量的基本性质和基本运算.考查了学生对三角函数和向量的知识的综合运用.
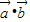 ,并利用二倍角的余弦化简整理.
,并利用二倍角的余弦化简整理.(2)根据(1)和题设向量的坐标求得函数f(x)的解析式,利用二倍角的余弦化简整理,然后利用x的范围确定cosx的范围,看λ∈[0,1],λ>1和λ<-1时根据二次函数的性质可确定函数的最小值,求得λ.
解答:解:(1)
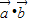 =
=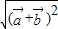 =
=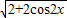 =2cosx(x∈[0,
=2cosx(x∈[0,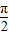 ])
])(2)由(1)知:f(x)=cos2x-4λcosx=2cos2x-4λcosx-1=2(cosx-λ)2-2λ2-1
∵
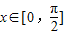
∴cosx∈[0,1],
当λ∈[0,1]时,f(x)min=-2λ2-1,而
 ,
,所以
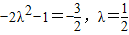 ,
,当λ<0时,
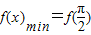 =2λ2-2λ2-1=-1,
=2λ2-2λ2-1=-1,而
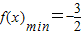 ,不符合题意.
,不符合题意.当λ>1时,f(x)min=f(0)=2-4λ-1=-4λ+1,而
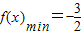
所以-4λ+1=-
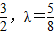 这与λ>1矛盾
这与λ>1矛盾综上述λ的值为
 .
.点评:本题主要考查了三角函数的最值,平面向量的基本性质和基本运算.考查了学生对三角函数和向量的知识的综合运用.

练习册系列答案
相关题目
 ,
, .且x
.且x
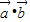 ;
; -2λ|
-2λ| |的最小值是-
|的最小值是- ,求λ的值.
,求λ的值. ,
, .且x
.且x
 ;
; -2λ|
-2λ| |的最小值是-
|的最小值是- ,求λ的值.
,求λ的值.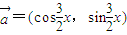 ,
,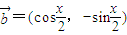 .且x
.且x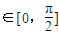
 ;
;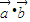 -2λ|
-2λ|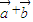 |的最小值是-
|的最小值是- ,求λ的值.
,求λ的值. ,
, .且x
.且x
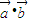 ;
; -2λ|
-2λ| |的最小值是-
|的最小值是- ,求λ的值.
,求λ的值.