题目内容
已知直线l:y=3x+2过抛物线y=ax2(a>0)的焦点.
(1)求抛物线方程;
(2)设抛物线的一条切线l1,若l1∥l,求切点坐标.
解:(1)抛物线y=ax2(a>0)的焦点为(0, ),-----------------3分
),-----------------3分
代入直线y=3x+2,得a=
(或用焦点坐标为(0,2)来解)抛物线方程x2=8y---------------------7分
(2)设切点坐标为(x0,y0),--------------------------------9分
由y= x,得y′=
x,得y′= x,即
x,即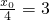 ,-------------------------12分
,-------------------------12分
得x0=12,代入抛物线方程得y0=18
切点坐标为(12,18)-----------------------15分
分析:(1)抛物线y=ax2(a>0)的焦点为(0, )代入直线y=3x+2可得 a 的值.
)代入直线y=3x+2可得 a 的值.
(2)设切点坐标为(x0,y0),由y= x,利用导数的几何意义切线的斜率
x,利用导数的几何意义切线的斜率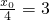 ,从而求出切点坐标.
,从而求出切点坐标.
点评:本题考查抛物线的标准方程,以及简单性质的应用,求出抛物线y=ax2(a>0)的焦点为(0, )是解题的关键.
)是解题的关键.
 ),-----------------3分
),-----------------3分代入直线y=3x+2,得a=

(或用焦点坐标为(0,2)来解)抛物线方程x2=8y---------------------7分
(2)设切点坐标为(x0,y0),--------------------------------9分
由y=
 x,得y′=
x,得y′= x,即
x,即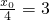 ,-------------------------12分
,-------------------------12分得x0=12,代入抛物线方程得y0=18
切点坐标为(12,18)-----------------------15分
分析:(1)抛物线y=ax2(a>0)的焦点为(0,
 )代入直线y=3x+2可得 a 的值.
)代入直线y=3x+2可得 a 的值.(2)设切点坐标为(x0,y0),由y=
 x,利用导数的几何意义切线的斜率
x,利用导数的几何意义切线的斜率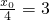 ,从而求出切点坐标.
,从而求出切点坐标.点评:本题考查抛物线的标准方程,以及简单性质的应用,求出抛物线y=ax2(a>0)的焦点为(0,
 )是解题的关键.
)是解题的关键. 
练习册系列答案
相关题目