题目内容
 已知水平地面上有一篮球,在斜平行光线的照射下,其阴影为一椭圆(如图),在平面直角坐标系中,O为原点,设椭圆的方程为
已知水平地面上有一篮球,在斜平行光线的照射下,其阴影为一椭圆(如图),在平面直角坐标系中,O为原点,设椭圆的方程为| x2 |
| a2 |
| y2 |
| b2 |
分析:在平行光线照射过程中,椭圆的短半轴长是圆的半径,球心到椭圆中心的距离是椭圆的长半轴,过球心向地面做垂线,垂足是H,得到一个直角三角形,得到要求的结果.
解答:解:在照射过程中,椭圆的短半轴长是圆的半径,
由图∠O′AB+∠O′BA=
(∠A′AB+∠B′BA)=
×180°=90°
∴∠AO′B=90°,由O是中点故有
球心到椭圆中心的距离是椭圆的长半轴,
过球心向地面做垂线,垂足是H,
在构成的直角三角形中,OO′2=OH2+O′H2,
∴OH=
,
故答案为:
,
由图∠O′AB+∠O′BA=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AO′B=90°,由O是中点故有
球心到椭圆中心的距离是椭圆的长半轴,
过球心向地面做垂线,垂足是H,
在构成的直角三角形中,OO′2=OH2+O′H2,
∴OH=
| a2-b2 |
故答案为:
| a2-b2 |
点评:本题考查圆锥曲线的实际背景及作用,解决本题的关键是看清楚在平行光线的照射下,投影中和球的量中,变与不变的量.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ),在斜平行光线的照射下,其阴影为一
),在斜平行光线的照射下,其阴影为一 为原点,
为原点, 所在直线为
所在直线为 轴,设椭圆的方程为
轴,设椭圆的方程为 ,篮球与地面的接触点为
,篮球与地面的接触点为 ,且
,且 ,则椭圆的离心率为______.
,则椭圆的离心率为______.
 已知水平地面上有一篮球,在斜平行光线的照射下,其阴影为一椭圆(如图),在平面直角坐标系中,O为原点,设椭圆的方程为
已知水平地面上有一篮球,在斜平行光线的照射下,其阴影为一椭圆(如图),在平面直角坐标系中,O为原点,设椭圆的方程为 (a>b>0),篮球与地面的接触点为H,则|OH|=________.
(a>b>0),篮球与地面的接触点为H,则|OH|=________.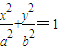 (a>b>0),篮球与地面的接触点为H,则|OH|= .
(a>b>0),篮球与地面的接触点为H,则|OH|= .
 ,篮球与地面的接触点为H,则|OH|=( )。
,篮球与地面的接触点为H,则|OH|=( )。