题目内容
在面积为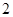 的正
的正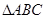 中,
中,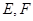 分别是
分别是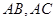 的中点,点
的中点,点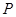 在直线
在直线 上,则
上,则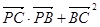 的最小值是___________。
的最小值是___________。
【答案】
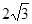
【解析】
试题分析:∵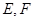 是
是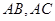 的中点,∴
的中点,∴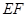 到
到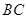 的距离为点
的距离为点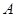 到
到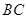 的距离的
的距离的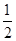 ,
,
∴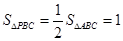 ,又
,又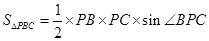 ,所以
,所以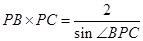 ,
,
由向量夹角公式,有: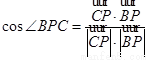 ,
,
∴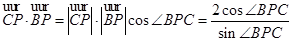 ,
,
由余弦定理,有: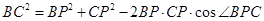 ,
,
显然,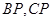 都是正数,所以
都是正数,所以 ,
,
所以 .
.
∴
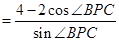
令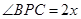 ,则:
,则:
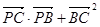
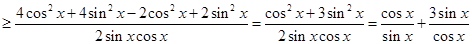
在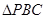 中,显然有
中,显然有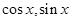 都是正数,所以
都是正数,所以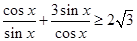 ,
,
所以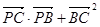 的最小值是
的最小值是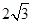 .
.
考点:本小题主要考查平面向量的数量积的应用、三角形面积公式的应用和余弦定理与基本不等式的综合应用,考查学生的综合应用能力和运算求解能力.
点评:要解决此类问题,需要牢固掌握多个知识点的内容并灵活应用,要有较强的逻辑思维能力和分析问题、解决问题的能力.

练习册系列答案
相关题目