题目内容
已知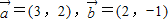
，若向量
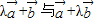夹角为锐角，则实数λ取值范围是 ．
【答案】分析：由已知可得，（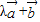
）
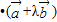=（3λ+2）×（3+2λ）+（2λ-1）×（2-λ）＞0且两向量不共线，解不等式可求
解答：解：∵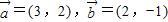
，
∴
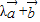=（3λ+2，2λ-1），
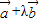=（3+2λ，2-λ）
∵向量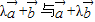
夹角为锐角
∴（
）
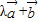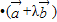=（3λ+2）×（3+2λ）+（2λ-1）×（2-λ）＞0
且（3λ+2）（2-λ）-（2λ-1）（3+2λ）≠0
整理可得，4λ2+18λ+4＞0且λ≠1
解不等式可得，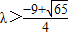
或
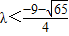且λ≠1
故答案为：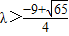
或
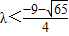且λ≠1
点评：本题主要考查了向量夹角公式的简单应用，要注意向量共线情况的考虑
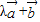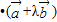）=（3λ+2）×（3+2λ）+（2λ-1）×（2-λ）＞0且两向量不共线，解不等式可求解答：解：∵
，∴
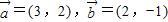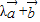=（3λ+2，2λ-1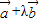），=（3+2λ，2-λ）∵向量
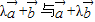夹角为锐角∴（
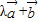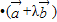）=（3λ+2）×（3+2λ）+（2λ-1）×（2-λ）＞0且（3λ+2）（2-λ）-（2λ-1）（3+2λ）≠0
整理可得，4λ2+18λ+4＞0且λ≠1
解不等式可得，
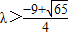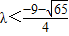或且λ≠1故答案为：
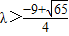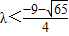或且λ≠1点评：本题主要考查了向量夹角公式的简单应用，要注意向量共线情况的考虑
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
，若
与
夹角为锐角，则实数
的取值范围为
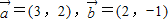，若向量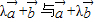
夹角为锐角，则实数λ取值范围是 ．
，若
与
夹角为锐角，则实数
的取值范围为
．
，若向量
夹角为锐角，则实数
取值范围