题目内容
 已知菱形ABCD,沿对角线BD将△ABD折起至△PBD处,P∉平面BCD,M是PC的中点.
已知菱形ABCD,沿对角线BD将△ABD折起至△PBD处,P∉平面BCD,M是PC的中点.(1)求证:PA∥平面BDM;
(2)求证:平面BDM⊥平面PAC.
分析:(1)设AC与BD交于点O,连MO,要证线面平行,利用线面平行的判定即可,只需证明MO∥PA
(2)要证面面垂直,只需要证明线面垂直,证明PC⊥平面BDM即可.
(2)要证面面垂直,只需要证明线面垂直,证明PC⊥平面BDM即可.
解答: 证明:(1)设AC与BD交于点O,连MO
证明:(1)设AC与BD交于点O,连MO
∵ABCD是菱形,∴O是AC的中点
又M是PC的中点
∴MO∥PA
∵MO?平面BDM,PA?平面BDM
∴PA∥平面BDM
(2)∵PB=PD=BC=CD
又M是PC的中点,∴BM⊥PC,DM⊥PC
∴PC⊥平面BDM
又PC?平面PAC
∴平面BDM⊥平面PAC
 证明:(1)设AC与BD交于点O,连MO
证明:(1)设AC与BD交于点O,连MO∵ABCD是菱形,∴O是AC的中点
又M是PC的中点
∴MO∥PA
∵MO?平面BDM,PA?平面BDM
∴PA∥平面BDM
(2)∵PB=PD=BC=CD
又M是PC的中点,∴BM⊥PC,DM⊥PC
∴PC⊥平面BDM
又PC?平面PAC
∴平面BDM⊥平面PAC
点评:本题以平面图形翻折为载体,考查线面平行,面面垂直,解题的关键是熟练运用线面平行,面面垂直的判定定理.

练习册系列答案
相关题目
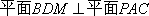
 已知菱形ABCD,沿对角线BD将△ABD折起至△PBD处,P∉平面BCD,M是PC的中点.
已知菱形ABCD,沿对角线BD将△ABD折起至△PBD处,P∉平面BCD,M是PC的中点.