题目内容
已知函数
．（1）若x∈R，求f（x）的最小正周期和单调递增区间；
（2）设
，求f（x）的值域．
【答案】分析：（1）利用两角和的正弦函数把函数化简为f（x）=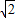
sin（2x+
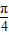），直接求出函数f（x）的最小正周期及单调区间；
（2）由
，求出2x+
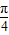的范围，进而求出正弦函数值的范围，再由解析式求出函数值域．
解答：解：（1）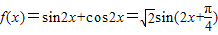
周期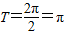
；
令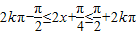
，得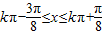
所以，单调递增区间为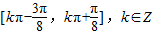
（2）若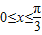
，则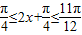
，
∴
，
即f（x）的值域为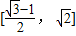
点评：本题的考点是正弦函数的单调性和求定区间上的值域，需要对解析式进行适当的化简成正弦型的函数，再利用整体思想求解．
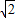sin（2x+ 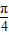），直接求出函数f（x）的最小正周期及单调区间；（2）由
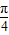，求出2x+ 的范围，进而求出正弦函数值的范围，再由解析式求出函数值域．解答：解：（1）
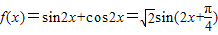
周期
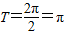；令
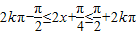，得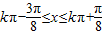所以，单调递增区间为
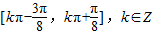
（2）若
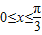，则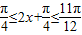，∴，即f（x）的值域为
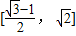
点评：本题的考点是正弦函数的单调性和求定区间上的值域，需要对解析式进行适当的化简成正弦型的函数，再利用整体思想求解．
练习册系列答案
相关题目
．（1）若x∈R，求f（x）的单调递增区间； （2）若x∈[0，
]时，f（x）的最大值为4，求a的值，并指出这时x的值
．
．
．
，求f（x）的值域．
，
取得极值，求实数
的值；
时，求
上的最小值；
，直线
都不是曲线
的切线，求实数