题目内容
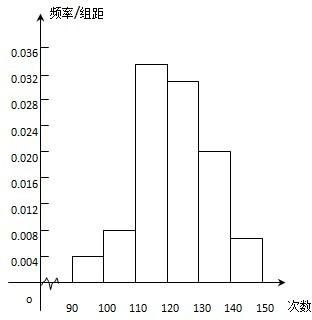
为了解高一学生的体能状况,某校抽取部分学生(样本容量为n)进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的高之比为2:4:17:15:9:3,第二小组频数为12.(Ⅰ)求出抽取的样本容量n和第二小组的频率p2;
(Ⅱ)试把给出的频率分布表填写完整;
(Ⅲ)若次数在110以上为体能达标,试通过样本估计全体高一学生的体能达标率.
| 分组 | 频数 | 频率 |
| [90,100) | ||
| [100,110) | 12 | |
| [110,120) | ||
| [120,130) | ||
| [130,140) | ||
| [140,150) | ||
| 合计 | 1 |
【答案】分析:(I)由已知中图中从左到右各小长方形的高之比为2:4:17:15:9:3,我们根据小长方形的高之比等于其频数比,也等于其频率比,构造关于n的方程,解方程即可得到样本容量n,再由第二小组频数为12,代入频率公式即可得到,第二小组的频率p2;
(II)根据已知中各小长方形的高之比为2:4:17:15:9:3,即各组频率之比为2:4:17:15:9:3,我们易根据(1)的结论,求出各组的频率及频数.
(III)样本中次数在110次以上指后四组的数据,根据(II)中数据,计算出满足条件的总频数,代入频率公式即可得到答案.
解答:解:(Ⅰ)小长方形的高之比等于其频数比,也等于其频率比,
所以,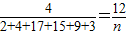
∴n=150
 (也可直接使用
(也可直接使用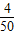 求解)
求解)
(Ⅱ)表中第一列数为6,12,51,45,27,9,150;第二列数为0.04,0.08,0.34,0.3,0.18,0.06,1
(Ⅲ)样本中次数在110次以上的共有51+45+27+9=132,频率为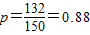
由此估计全体高一学生的体能达标率为0.88.
点评:本题考查的知识点是频率分布直方图及其应用,其中根据已知条件,及频率分布直方图中各小长方形的高之比等于其频数比,也等于其频率比,构造对应的方程是解答本题的关键.
(II)根据已知中各小长方形的高之比为2:4:17:15:9:3,即各组频率之比为2:4:17:15:9:3,我们易根据(1)的结论,求出各组的频率及频数.
(III)样本中次数在110次以上指后四组的数据,根据(II)中数据,计算出满足条件的总频数,代入频率公式即可得到答案.
解答:解:(Ⅰ)小长方形的高之比等于其频数比,也等于其频率比,
所以,
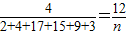
∴n=150
 (也可直接使用
(也可直接使用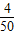 求解)
求解)(Ⅱ)表中第一列数为6,12,51,45,27,9,150;第二列数为0.04,0.08,0.34,0.3,0.18,0.06,1
(Ⅲ)样本中次数在110次以上的共有51+45+27+9=132,频率为
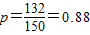
由此估计全体高一学生的体能达标率为0.88.
点评:本题考查的知识点是频率分布直方图及其应用,其中根据已知条件,及频率分布直方图中各小长方形的高之比等于其频数比,也等于其频率比,构造对应的方程是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
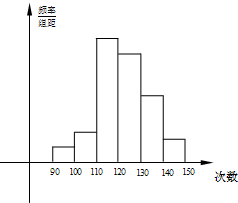 为了解高一学生的体能状况,某校抽取部分学生(样本容量为n)进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的高之比为2:4:17:15:9:3,第二小组频数为12.
为了解高一学生的体能状况,某校抽取部分学生(样本容量为n)进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的高之比为2:4:17:15:9:3,第二小组频数为12.(Ⅰ)求出抽取的样本容量n和第二小组的频率p2;
(Ⅱ)试把给出的频率分布表填写完整;
(Ⅲ)若次数在110以上为体能达标,试通过样本估计全体高一学生的体能达标率.
| 分组 | 频数 | 频率 |
| [90,100) | ||
| [100,110) | 12 | |
| [110,120) | ||
| [120,130) | ||
| [130,140) | ||
| [140,150) | ||
| 合计 | 1 |