题目内容
已知函数: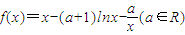 ,
,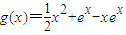
(1)当x∈[1,e]时,求f(x)的最小值;
(2)当a<1时,若存在
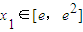 ,使得对任意的x2∈[-2,0],f(x1)<g(x2)恒成立,求a的取值范围.
,使得对任意的x2∈[-2,0],f(x1)<g(x2)恒成立,求a的取值范围.
【答案】分析:(1)求出f(x)的定义域,求导数f′(x),得其极值点,按照极值点a在[1,e]的左侧、内部、右侧三种情况进行讨论,可得其最小值;
(2)存在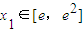 ,使得对任意的x2∈[-2,0],f(x1)<g(x2)恒成立,即 f(x)min<g(x)min,由(1)知f(x)在[e,e2]上递增,可得f(x)min,利用导数可判断g(x)在[-2,0]上的单调性,可得g(x)min,由 f(x)min<g(x)min,可求得a的范围;
,使得对任意的x2∈[-2,0],f(x1)<g(x2)恒成立,即 f(x)min<g(x)min,由(1)知f(x)在[e,e2]上递增,可得f(x)min,利用导数可判断g(x)在[-2,0]上的单调性,可得g(x)min,由 f(x)min<g(x)min,可求得a的范围;
解答:解:(1)f(x)的定义域为(0,+∞),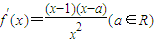 ,
,
当a≤1时,x∈[1,e],f′(x)≥0,f(x)为增函数,
所以f(x)min=f(1)=1-a;
当1<a<e时,x∈[1,a],f′(x)≤0,f(x)为减函数,x∈[a,e],f′(x)≥0,f(x)为增函数,
所以f(x)min=f(a)=a-(a+1)lna-1;
当a≥e时,x∈[1,e],f′(x)≤0,f(x)为减函数,
所以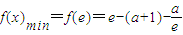 ;
;
综上,当a≤1时,f(x)min=1-a;当1<a<e时,f(x)min=a-(a+1)lna-1;当a≥e时,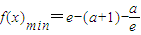 ;
;
(2)存在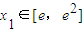 ,使得对任意的x2∈[-2,0],f(x1)<g(x2)恒成立,即 f(x)min<g(x)min,
,使得对任意的x2∈[-2,0],f(x1)<g(x2)恒成立,即 f(x)min<g(x)min,
当a<1时,由(1)可知,x∈[e,e2],f(x)为增函数,
∴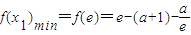 ,
,
g′(x)=x+ex-xex-ex=x(1-ex),
当x∈[-2,0]时g′(x)≤0,g(x)为减函数,g(x)min=g(0)=1,
∴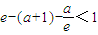 ,
,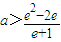 ,
,
∴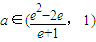 .
.
点评:本题考查利用导数研究函数的单调性、求闭区间上函数的最值,考查分类讨论思想,考查学生分析解决问题的能力,恒成立问题往往转化为函数的最值加以解决.
(2)存在
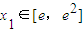 ,使得对任意的x2∈[-2,0],f(x1)<g(x2)恒成立,即 f(x)min<g(x)min,由(1)知f(x)在[e,e2]上递增,可得f(x)min,利用导数可判断g(x)在[-2,0]上的单调性,可得g(x)min,由 f(x)min<g(x)min,可求得a的范围;
,使得对任意的x2∈[-2,0],f(x1)<g(x2)恒成立,即 f(x)min<g(x)min,由(1)知f(x)在[e,e2]上递增,可得f(x)min,利用导数可判断g(x)在[-2,0]上的单调性,可得g(x)min,由 f(x)min<g(x)min,可求得a的范围;解答:解:(1)f(x)的定义域为(0,+∞),
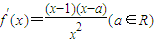 ,
,当a≤1时,x∈[1,e],f′(x)≥0,f(x)为增函数,
所以f(x)min=f(1)=1-a;
当1<a<e时,x∈[1,a],f′(x)≤0,f(x)为减函数,x∈[a,e],f′(x)≥0,f(x)为增函数,
所以f(x)min=f(a)=a-(a+1)lna-1;
当a≥e时,x∈[1,e],f′(x)≤0,f(x)为减函数,
所以
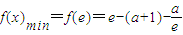 ;
;综上,当a≤1时,f(x)min=1-a;当1<a<e时,f(x)min=a-(a+1)lna-1;当a≥e时,
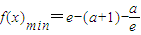 ;
;(2)存在
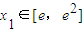 ,使得对任意的x2∈[-2,0],f(x1)<g(x2)恒成立,即 f(x)min<g(x)min,
,使得对任意的x2∈[-2,0],f(x1)<g(x2)恒成立,即 f(x)min<g(x)min,当a<1时,由(1)可知,x∈[e,e2],f(x)为增函数,
∴
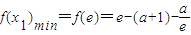 ,
,g′(x)=x+ex-xex-ex=x(1-ex),
当x∈[-2,0]时g′(x)≤0,g(x)为减函数,g(x)min=g(0)=1,
∴
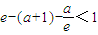 ,
,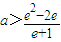 ,
,∴
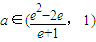 .
.点评:本题考查利用导数研究函数的单调性、求闭区间上函数的最值,考查分类讨论思想,考查学生分析解决问题的能力,恒成立问题往往转化为函数的最值加以解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
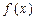 ,如果满足:对任意
,如果满足:对任意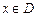 ,存在常数
,存在常数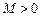 ,都有
,都有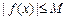 成立,则称
成立,则称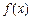 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数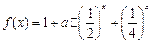 ;
;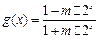 .
.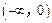 上的值域,并判断函数
上的值域,并判断函数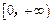 上是以3为上界的
上是以3为上界的 有界函数,求实数a的取值范围;
有界函数,求实数a的取值范围;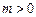 ,函
,函 数
数 在
在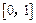 上的上界是
上的上界是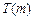 ,求
,求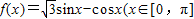 ),
),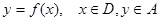 ;
;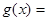
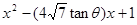 ,
,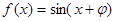 为偶函数时,求
为偶函数时,求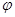 的值。
的值。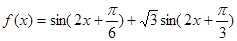 时,
时,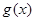 在
在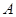 上是单调递增函数,求
上是单调递增函数,求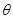 的取值范围。
的取值范围。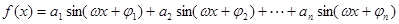 时,(其中
时,(其中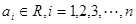 ,
,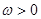 ),若
),若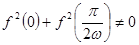 ,且函数
,且函数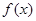 的图像关于点
的图像关于点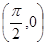 对称,在
对称,在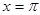 处取得最小值,试探讨
处取得最小值,试探讨 应该满足的条件。
应该满足的条件。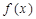 ,如果满足:对任意
,如果满足:对任意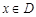 ,存在常数
,存在常数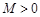 ,都有
,都有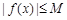 成立,则称
成立,则称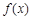 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数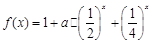 ;
;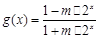 .
.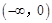 上的值域,并判断函数
上的值域,并判断函数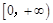 上是以3为上界的有界函数,求实数a的取值范围;
上是以3为上界的有界函数,求实数a的取值范围;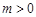 ,函数
,函数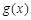 在
在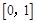 上的上界是
上的上界是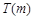 ,求
,求 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数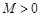 ,都有
,都有 成立,则称
成立,则称 是D上的有界函数,其中M称为函数
是D上的有界函数,其中M称为函数 ;
; .
. 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界的有界函数,求实数a的取值范围;
上是以3为上界的有界函数,求实数a的取值范围; ,函数
,函数 在
在 上的上界是
上的上界是 ,求
,求