题目内容
 从以下两个小题中选做一题(只能做其中一个,做两个按得分最低的记分).
从以下两个小题中选做一题(只能做其中一个,做两个按得分最低的记分).(1)自极点O向直线l作垂线,垂足是H((2,
| π | 3 |
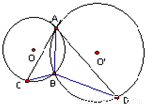
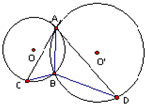
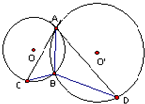
(2)如图,⊙O和⊙O'都经过A、B两点,AC是⊙O'的切线,交⊙O于点C,AD是⊙O的切线,交⊙O'于点D,若BC=2,BD=6,则AB的长为
分析:(1)此题可直接在极坐标系中求出直线l的极坐标方程.设直线l上任一点的极坐标为(ρ,θ),再结合直角三角形的边角关系即可求得ρ与θ的关系式即为所求直线l的极坐标方程.
(2)由AC是圆O'的切线,AD是圆O的切线,利用圆的弦切角等于所夹弧所对的圆周角,得到三角形ABC与三角形ABD相似,由相似得到三角形的对应边成比例得到一个关系式,把BC和AB的值代入关系式即可求出BD的值.
(2)由AC是圆O'的切线,AD是圆O的切线,利用圆的弦切角等于所夹弧所对的圆周角,得到三角形ABC与三角形ABD相似,由相似得到三角形的对应边成比例得到一个关系式,把BC和AB的值代入关系式即可求出BD的值.
解答: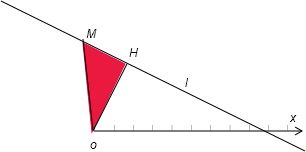 (1)解:如图,
(1)解:如图,
极点O向直线l作垂线,垂足是H,
设直线l上任一点的极坐标为(ρ,θ),
在直角三角形OHM中,∠HOM=ρ-
,
OH=OMcos∠HOM,
∴ρcos(θ-
)=2
或展开得:ρcosθ+3ρsinθ-4=0.
故答案为:ρcos(θ-
)=2或 ρcosθ+3ρsinθ-4=0.
(2)解:因为AC是圆O′的切线,
∴∠CAB=∠D,
∵AD是圆O的切线,
∴∠BAD=∠C,
∴△ABC∽△DBA,
∴
=
,又BC=2,BD=6,
则AB的长为2
故答案为:2
.
 (1)解:如图,
(1)解:如图,极点O向直线l作垂线,垂足是H,
设直线l上任一点的极坐标为(ρ,θ),
在直角三角形OHM中,∠HOM=ρ-
| π |
| 3 |
OH=OMcos∠HOM,
∴ρcos(θ-
| π |
| 3 |
或展开得:ρcosθ+3ρsinθ-4=0.
故答案为:ρcos(θ-
| π |
| 3 |
(2)解:因为AC是圆O′的切线,
∴∠CAB=∠D,
∵AD是圆O的切线,
∴∠BAD=∠C,
∴△ABC∽△DBA,
∴
| AB |
| BC |
| BD |
| AB |
则AB的长为2
| 3 |
故答案为:2
| 3 |
点评:(1)本题考查简单曲线的极坐标方程,能在极坐标系中用极坐标刻画点的位置,体会在极坐标系和平面直角坐标系中刻画点的位置的区别,能进行极坐标和直角坐标的互化.
(2)此题考查学生灵活运用弦切角定理以及三角形相似对应边成比例化简求值,是一道中档题.
(2)此题考查学生灵活运用弦切角定理以及三角形相似对应边成比例化简求值,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 从以下两个小题中选做一题(只能做其中一个,做两个按得分最低的记分).
从以下两个小题中选做一题(只能做其中一个,做两个按得分最低的记分).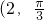 ),则直线l的极坐标方程为________.
),则直线l的极坐标方程为________.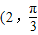 ),则直线l的极坐标方程为 .
),则直线l的极坐标方程为 .