题目内容
(本题满分10分)甲乙两地相距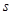 km,汽车从甲地匀速行驶到乙地,速度不得超过
km,汽车从甲地匀速行驶到乙地,速度不得超过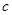 km/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度
km/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度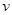 km/h的平方成正比,比例系数为
km/h的平方成正比,比例系数为 ,固定部分为
,固定部分为 元.
元.
(1)把全程运输成本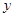 (元)表示为
(元)表示为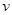 速度(千米/时)的函数,并指出这个函数的定义域;
速度(千米/时)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
【答案】
(1)所求函数及其定义域为y=s(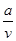 +bv),v∈
+bv),v∈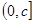 .
.
(2)为使全程运输成本y最小,当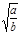 ≤c时,行驶速度为v=
≤c时,行驶速度为v=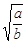 ;当
;当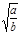 >c时,行驶速度为v=c.
>c时,行驶速度为v=c.
【解析】解:(1)依题意知,汽车从甲地匀速行驶到乙地所用时间为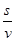 ,全程运输成本为y=a·
,全程运输成本为y=a·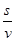 +bv2·
+bv2·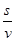 =s(
=s(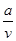 +bv).
+bv).
故所求函数及其定义域为y=s(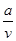 +bv),v∈
+bv),v∈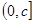 .
.
(2)依题意知s,a,b,v都是正数,故有s(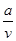 +bv)≥2s
+bv)≥2s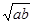 .当且仅当
.当且仅当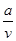 =bv,即v=
=bv,即v=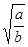 时上式中等号成立.
时上式中等号成立.
①当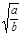 ≤c时,则当v=
≤c时,则当v=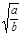 时全程运输成本最小;
时全程运输成本最小;
②当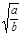 >c时,则当v∈
>c时,则当v∈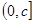 时有s(
时有s(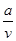 +bv)-s(
+bv)-s(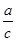 +bc)=s[(
+bc)=s[(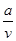 -
-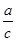 )+(bv-bc)]=
)+(bv-bc)]=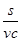 (c-v)(a-bcv).
(c-v)(a-bcv).
∵c-v≥0且a>bc2,故有a-bcv≥a-bc2>0,∴s(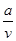 +bv)≥s(
+bv)≥s(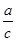 +bc),当且仅当v=c时等号成立.
+bc),当且仅当v=c时等号成立.
即当v=c时全程运输成本最小.
综上知,为使全程运输成本y最小,当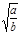 ≤c时,行驶速度为v=
≤c时,行驶速度为v=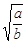 ;当
;当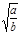 >c时,行驶速度为v=c.
>c时,行驶速度为v=c.

练习册系列答案
相关题目
 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为 ,且各人答题正确与否相互之间没有影响.用
,且各人答题正确与否相互之间没有影响.用 表示甲队的总得分.
表示甲队的总得分. 表示“甲、乙两个队总得分之和等于3”这一事件,用
表示“甲、乙两个队总得分之和等于3”这一事件,用 表示“甲队总得分大于乙队总得分”这一事件,求
表示“甲队总得分大于乙队总得分”这一事件,求 .
. ,且面试是否合格互不影响,求:
,且面试是否合格互不影响,求: