题目内容
15.设f(x)是定义在R上的奇函数,且y=f(2x-1)的周期为4,若f(1)=2.求f(2015)=-2.分析 根据f(2x-1)的周期,求得f(x)的周期,再根据函数的奇偶性,确定f(2015)的值.
解答 解:∵f(2x-1)是周期为4的函数,
∴f[2(x+4)-1]=f(2x-1),
即f(2x+7)=f(2x-1),两边括号内的数值相差8个单位,
所以,y=f(x)是一个周期为8的函数,
f(2015)=f(251×8+7)=f(7)=f(-1)
又∵f(x)为奇函数,
∴f(-1)=-f(1)=-2,
故f(2015)=-2.
点评 本题主要考查了函数周期的确定和函数奇偶性的应用,其中函数周期的确定容易出错,用到整体思想,属于容易题.

练习册系列答案
相关题目
6.已知x2+y2=4,x>0,y>0,且loga(2+x)=m,loga$\frac{1}{2-x}$=n,则logay等于( )
| A. | m+n | B. | m-n | C. | $\frac{1}{2}$(m+n) | D. | $\frac{1}{2}$(m-n) |
3.下列函数在(-∞,+∞)上为单调函数的是( )
| A. | y=x2-x | B. | y=|x| | C. | y=x3+2x | D. | y=sinx |
20.已知函数y=f(x)图象上每个点的纵坐标保持不变,横坐标伸长到原来2倍,然后再将整个图象沿x轴左平移$\frac{π}{2}$个单位,沿y轴向下平移1个单位,得到函数y=$\frac{1}{2}$sinx,则y=f(x)的表达式为( )
| A. | y=$\frac{1}{2}$sin(2x+$\frac{π}{2}$)+1 | B. | y=$\frac{1}{2}$sin(2x-$\frac{π}{2}$)+1 | C. | y=$\frac{1}{2}$sin(2x-$\frac{π}{4}$)+1 | D. | y=$\frac{1}{2}$sin($\frac{1}{2}$x+$\frac{π}{4}$)+1 |
5.曲线y=x(x-1)(x-2)…(x-5)在x=0处的导数为( )
| A. | 120 | B. | -120 | C. | 60 | D. | -60 |
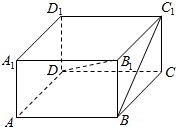 在长方体ABCD-A1B1C1D1中,底面边长AB=3m,BC=4m,高BB1=5m,求:
在长方体ABCD-A1B1C1D1中,底面边长AB=3m,BC=4m,高BB1=5m,求: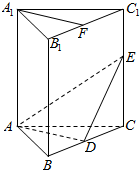 如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,F为B1C1的中点,D,E分别是棱BC,CC1上的点,且AD⊥BC.
如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,F为B1C1的中点,D,E分别是棱BC,CC1上的点,且AD⊥BC.