题目内容
选修4-4:参考方程与极坐标
分别在下列两种情况下,把参数方程
化为普通方程:
(1)θ为参数,t为常数;
(2)t为参数,θ为常数.
分别在下列两种情况下,把参数方程
|
(1)θ为参数,t为常数;
(2)t为参数,θ为常数.
分析:(1)θ为参数,t为常数时,考虑用sin2θ+cos2θ=1,消去θ.
(2)t为参数,θ为常数时,可考虑根据et•e-t=1,消去t.
(2)t为参数,θ为常数时,可考虑根据et•e-t=1,消去t.
解答:解:(1)当t=0时,y=0,x=cosθ,即|x|≤1,且y=0;…(2分)
当t≠0时,cosθ=
,sinθ=
…(4分)
而cos2θ+sin2θ=1,即
+
=1…(5分)
(2)当θ=kπ,k∈Z时,y=0,x=±
(et+e-t),即|x|≥1,且y=0…(6分);
当θ=kπ+
,k∈Z时,x=0,y=±
(et-e-t),即x=0;…(7分)
当θ≠
,k∈Z时,得
,即
…(9分)
得2et•2e-t=(
+
)(
-
),即
-
=1.…(10分)
当t≠0时,cosθ=
| x | ||
|
| y | ||
|
而cos2θ+sin2θ=1,即
| x2 | ||
|
| y2 | ||
|
(2)当θ=kπ,k∈Z时,y=0,x=±
| 1 |
| 2 |
当θ=kπ+
| π |
| 2 |
| 1 |
| 2 |
当θ≠
| kπ |
| 2 |
|
|
得2et•2e-t=(
| 2x |
| cosθ |
| 2y |
| sinθ |
| 2x |
| cosθ |
| 2y |
| sinθ |
| x2 |
| cos2θ |
| y2 |
| sin2θ |
点评:本题考查参数方程转化成普通方程,关键在于正确的消参.考查计算、分类讨论的意识和能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
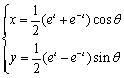 化为普通方程:
化为普通方程: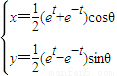 化为普通方程:
化为普通方程: