题目内容
已知函数 的图象经过原点,且关于点(-1,1)成中心对称.
的图象经过原点,且关于点(-1,1)成中心对称.(1)求函数f(x)的解析式;
(2)若数列{an}满足an>0,a1=1,
 ,求数列{an}的通项公式;
,求数列{an}的通项公式;(3)在(2)的条件下,设数列{an}的前n项和为Sn,试判断Sn与2的大小关系,并证明你的结论.
【答案】分析:(1)f(0)=0,可求b=0.所以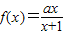 .由函数
.由函数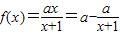 图象关于点(-1,1)成中心对称,可求a
图象关于点(-1,1)成中心对称,可求a
(2)因为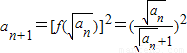 ,且an>0,整理可得
,且an>0,整理可得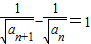 .从而得到数列
.从而得到数列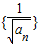 是等差数列,可求
是等差数列,可求
(3)由n≥2时,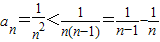 ,从而放缩结合裂项求和即可求
,从而放缩结合裂项求和即可求
解答:解:(1)因为函数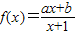 的图象经过原点,
的图象经过原点,
所以f(0)=0,即b=0.所以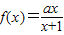 .
.
因为函数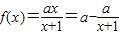 的图象关于点(-1,1)成中心对称,
的图象关于点(-1,1)成中心对称,
所以a=1.所以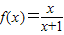 .
.
(2)因为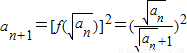 ,且an>0,
,且an>0,
所以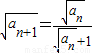 ,即
,即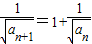 ,即
,即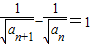 .
.
所以数列 是首项为
是首项为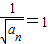 ,公差为1的等差数列.
,公差为1的等差数列.
所以 ,所以
,所以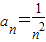 (n∈N*).
(n∈N*).
(3)当n=1时,S1=a1=1<2;
当n≥2时,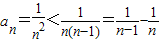 ,
,
所以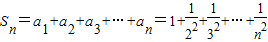
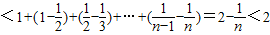 .
.
综上所述,Sn<2(n∈N*).
点评:本题以函数中由函数的性质求解函数解析式为载体,重点考查了利用构造特殊数列(等差、等比)求解数列的通项公式,及裂项求和,要注意放缩法在解题中的应用.
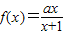 .由函数
.由函数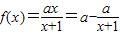 图象关于点(-1,1)成中心对称,可求a
图象关于点(-1,1)成中心对称,可求a(2)因为
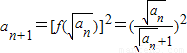 ,且an>0,整理可得
,且an>0,整理可得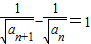 .从而得到数列
.从而得到数列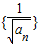 是等差数列,可求
是等差数列,可求(3)由n≥2时,
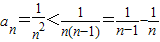 ,从而放缩结合裂项求和即可求
,从而放缩结合裂项求和即可求解答:解:(1)因为函数
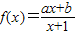 的图象经过原点,
的图象经过原点,所以f(0)=0,即b=0.所以
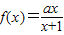 .
.因为函数
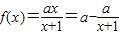 的图象关于点(-1,1)成中心对称,
的图象关于点(-1,1)成中心对称,所以a=1.所以
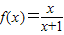 .
.(2)因为
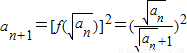 ,且an>0,
,且an>0,所以
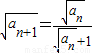 ,即
,即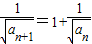 ,即
,即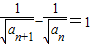 .
.所以数列
 是首项为
是首项为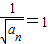 ,公差为1的等差数列.
,公差为1的等差数列.所以
 ,所以
,所以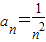 (n∈N*).
(n∈N*).(3)当n=1时,S1=a1=1<2;
当n≥2时,
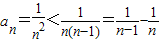 ,
,所以
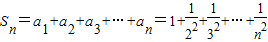
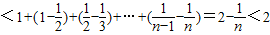 .
.综上所述,Sn<2(n∈N*).
点评:本题以函数中由函数的性质求解函数解析式为载体,重点考查了利用构造特殊数列(等差、等比)求解数列的通项公式,及裂项求和,要注意放缩法在解题中的应用.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
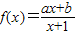 的图象经过原点,且关于点(-1,1)成中心对称.
的图象经过原点,且关于点(-1,1)成中心对称. ,求数列{an}的通项公式;
,求数列{an}的通项公式;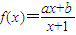 的图象经过原点,且关于点(-1,1)成中心对称.
的图象经过原点,且关于点(-1,1)成中心对称.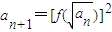 ,求数列{an}的通项公式;
,求数列{an}的通项公式;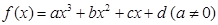 的图象经过原点,
的图象经过原点,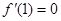 若
若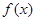 在
在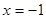 取得极大值2。
取得极大值2。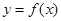 的解析式;
的解析式; ,求
,求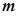 的最大值。
的最大值。 的图象经过原点,
的图象经过原点, 若
若 在
在 取得极大值2。
取得极大值2。 的解析式;
的解析式;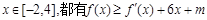 ,求
,求 的最大值。
的最大值。