题目内容
已知函数 .
.
⑴求函数 在
在 处的切线方程;
处的切线方程;
⑵当 时,求证:
时,求证: ;
;
⑶若 ,且
,且 对任意
对任意 恒成立,求k的最大值.
恒成立,求k的最大值.
⑴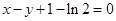 ;⑵详见解析;⑶
;⑵详见解析;⑶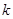 的最大值是3.
的最大值是3.
解析试题分析:⑴曲线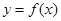 在点
在点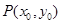 处的切线方程为:
处的切线方程为: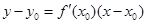 ,所以求出导数及切点即得切线方程;⑵不失一般性,左右两边作差得:
,所以求出导数及切点即得切线方程;⑵不失一般性,左右两边作差得: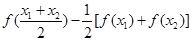
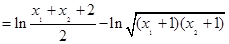 ,接下来用重要不等式比较真数的大小即可.⑶首先分离参数.由于
,接下来用重要不等式比较真数的大小即可.⑶首先分离参数.由于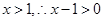 ,所以
,所以 可变为
可变为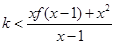 .令
.令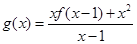 ,则
,则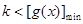 ,注意到
,注意到 ,则
,则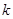 取最大整数即可.接下来就利用导数求则
取最大整数即可.接下来就利用导数求则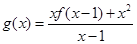 的最小值.
的最小值.
试题解析:⑴
∴故切线斜率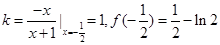
∴所切线方程: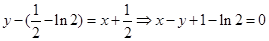 . .3分
. .3分
⑵由题可知:
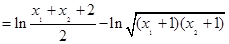
∵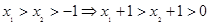
∴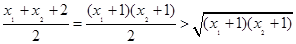
∴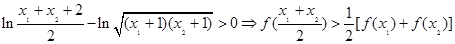 . 8分
. 8分
⑶令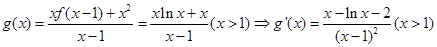
令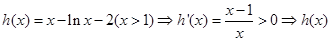 在
在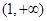 上单调递增.
上单调递增.
∵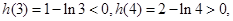
∴所以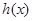 存在唯一零点
存在唯一零点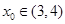 ,即
,即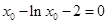 .
.
当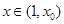 时,
时,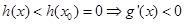 ;
;
当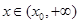 时,
时,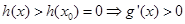 ;
;
∴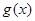 在
在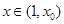 时单调递减;在
时单调递减;在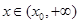 时,单调递增;
时,单调递增;
∴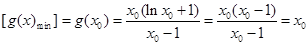
由题意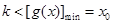 ,又因为
,又因为 ,所以
,所以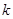 的最大值是3. 14分
的最大值是3. 14分
考点:1、导数的应用;2、导数与不等式.

练习册系列答案
相关题目
 ,
,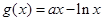 ,其中
,其中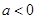 ,
,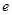 为自然对数的底数.
为自然对数的底数.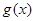 在
在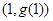 处的切线
处的切线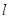 与直线
与直线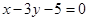 垂直,求
垂直,求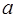 的值;
的值;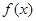 在
在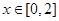 上的最小值;
上的最小值;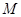 ,使得
,使得 .当
.当 时,函数
时,函数 取得极值
取得极值 .
. 有3个解,求实数
有3个解,求实数 的取值范围.
的取值范围.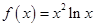 .
. 的单调区间;
的单调区间;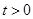 ,存在唯一的
,存在唯一的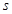 ,使
,使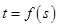 ;
;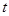 的函数为
的函数为 ,证明:当
,证明:当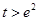 时,有
时,有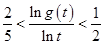 .
.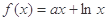 ,其中a为常数.
,其中a为常数. 时,求
时,求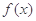 的最大值;
的最大值;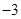 ,求a的值;
,求a的值;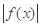 =
=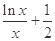 是否有实数解.
是否有实数解.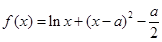 ,
,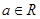 .
. 在
在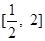 上单调递增,求实数
上单调递增,求实数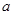 的取值范围;
的取值范围;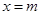 为函数
为函数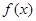 的图象与
的图象与 轴交于
轴交于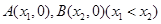 两点,且
两点,且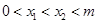 ,
,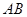 中点为
中点为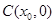 ,
,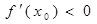 .
.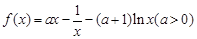 .
. 在点
在点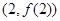 处的切线与直线
处的切线与直线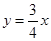 平行,求实数
平行,求实数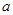 的值;
的值;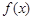 在
在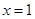 处取得极小值,且
处取得极小值,且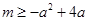 ,求实数
,求实数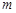 的取值范围.
的取值范围.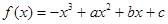 在
在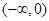 上是减函数,在
上是减函数,在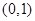 上是增函数,函数
上是增函数,函数 在
在 上有三个零点,且
上有三个零点,且 是其中一个零点.
是其中一个零点.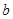 的值;
的值;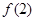 的取值范围;
的取值范围;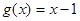 ,且
,且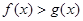 的解集为
的解集为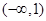 ,求实数
,求实数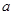 的取值范围.
的取值范围.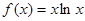 .
. 的单调区间和极值;
的单调区间和极值;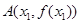 ,
,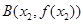 ,且
,且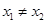 ,证明:
,证明: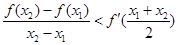 .
.