题目内容
设x，y∈（0，2]，已知xy=2，且6-2x-y≥a（2-x）（4-y）恒成立，那么实数a的取值范围是 ．
【答案】分析：先换元，令2x+y=t并求出它的取值范围，然后利用分离法将参数a分离出来，求不等式另一侧的最值即可．
解答：解：令2x+y=t，则t∈[4，5]
∵6-2x-y≥a（2-x）（4-y）
∴6-t≥a（10-2t）即a≤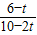
∴a≤（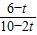
）min=1
故答案为（-∞，1]
点评：本题主要考查了函数恒成立问题，以及换元法的应用，属于基础题．
解答：解：令2x+y=t，则t∈[4，5]
∵6-2x-y≥a（2-x）（4-y）
∴6-t≥a（10-2t）即a≤
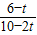
∴a≤（
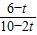）min=1故答案为（-∞，1]
点评：本题主要考查了函数恒成立问题，以及换元法的应用，属于基础题．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目