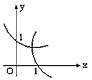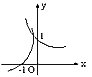题目内容
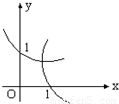
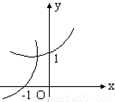
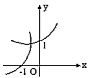
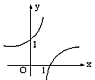
设0＜a＜1，在同一直角坐标系中，函数y=a-x与y=loga（-x）的图象是
- A.
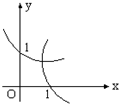
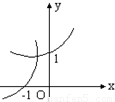
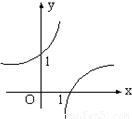
- B.
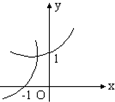
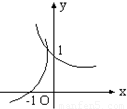
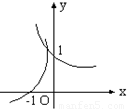
- C.
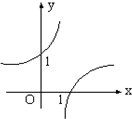
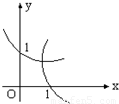
- D.
B
分析：利用指数函数、对数函数的图象和性质逐项判断即可得到答案．
解答：因为0＜a＜1，所以
＞1，故y=a-x=
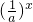单调递增，且y=a-x的图象过（0，1）点；
又y=loga（-x）与y=logax的图象关于y轴对称，且y=logax单调递减，图象过点（1，0），
所以y=loga（-x）单调递增，图象过点（-1，0）．
故选B．
点评：本题考查了指数函数、对数函数的图象，对于关于图象的选择题，注意特殊点的应用．
分析：利用指数函数、对数函数的图象和性质逐项判断即可得到答案．
解答：因为0＜a＜1，所以
＞1，故y=a-x=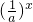单调递增，且y=a-x的图象过（0，1）点；又y=loga（-x）与y=logax的图象关于y轴对称，且y=logax单调递减，图象过点（1，0），
所以y=loga（-x）单调递增，图象过点（-1，0）．
故选B．
点评：本题考查了指数函数、对数函数的图象，对于关于图象的选择题，注意特殊点的应用．
练习册系列答案
相关题目
