题目内容
设f(x)=lg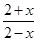 ,则f
,则f +f
+f 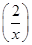 的定义域为( )
的定义域为( )
| A.(-4,0)∪(0,4) | B.(-4,-1)∪(1,4) |
| C.(-2,-1)∪(1,2) | D.(-4,-2)∪(2,4) |
B
解析试题分析:由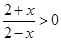 ,得f(x)的定义域为{x|-2<x<2}.
,得f(x)的定义域为{x|-2<x<2}.
故-2<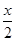 <2,-2<
<2,-2<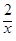 <2.解得x∈(-4,-1)∪(1, 4).
<2.解得x∈(-4,-1)∪(1, 4).
考点:1、对数函数;2、解不等式.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
已知函数 的定义域是R,则实数
的定义域是R,则实数 的取值范围是( )
的取值范围是( )
| A.(0,2) | B.(-2,2) | C.[-2,2] | D. |
设 是定义在R上的偶函数,且在
是定义在R上的偶函数,且在 上是增函数,设
上是增函数,设 ,则
,则 的大小关系是( )
的大小关系是( )
A. | B. | C. | D. |
已知函数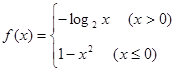 ,则不等式
,则不等式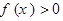 的解集为( )
的解集为( )
A.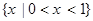 | B.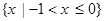 | C.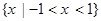 | D.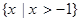 |
若函数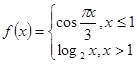 ,则
,则 ( )
( )
A.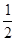 | B.1 | C.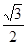 | D.3 |
定义运算 ,如
,如 ,令
,令 ,则
,则 为( )
为( )
A.奇函数,值域 | B.偶函数,值域 |
C.非奇非偶函数,值域 | D.偶函数,值域 |
设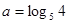 ,
,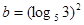 ,
,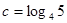 则 ( )
则 ( )
A.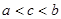 | B.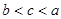 | C.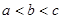 | D. |
设 ,
, (
( ,且
,且 ),若
),若 的图像与
的图像与 的图像有且仅有两个不同的公共点从左向右分别为
的图像有且仅有两个不同的公共点从左向右分别为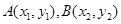 ,则下列判断正确的是( )
,则下列判断正确的是( )
A. 时 时 |
B. 时 时 |
C. 时 时 |
D. 时 时 |
已知函数 ,若
,若 ,则实数
,则实数 等于( )
等于( )
A. | B. | C.2 | D.4 |