题目内容
 如图所示,过抛物线C:y2=2px(p>0)的焦点F作直线交C于A、B两点,过A、B分别向C的准线l作垂线,垂足为A′,B′,已知四边形AA′B′F与BB′A′F的面积分别为15和7,则△A′B′F的面积为
如图所示,过抛物线C:y2=2px(p>0)的焦点F作直线交C于A、B两点,过A、B分别向C的准线l作垂线,垂足为A′,B′,已知四边形AA′B′F与BB′A′F的面积分别为15和7,则△A′B′F的面积为6
6
.分析:设△A′B′F的面积为S,直线AB:x=my+
,代入抛物线方程,利用韦达定理,计算S△AA'F,S△BB'F,求出面积的积,利用四边形AA′B′F与BB′A′F的面积分别为15和7,建立方程,即可求得△A′B′F的面积.
| p |
| 2 |
解答:解:设△A′B′F的面积为S,直线AB:x=my+
,代入抛物线方程,消元可得y2-2pmy-p2=0
设A(x1,y1) B(x2,y2),则y1y2=-p2,y1+y2=2pm
S△AA'F=
|AA'|×|y1|=
|x1+
||y1|=
(
+
)|y1|
S△BB'F=
|BB'|×|y2|=
|x2+
||y2|=
(
+
)|y2|
∴
(
+
)|y1|×
(
+
)|y2|=
(
+
+
)=
(m2+1)
S△A′B′F=
|y1-y2|=p2
=S
∵四边形AA′B′F与BB′A′F的面积分别为15和7
∴
(m2+1)=(15-S)(7-S)
∴
S2=(15-S)(7-S)
∴
S2-22S+105=0
∴S=6
故答案为:6
| p |
| 2 |
设A(x1,y1) B(x2,y2),则y1y2=-p2,y1+y2=2pm
S△AA'F=
| 1 |
| 2 |
| 1 |
| 2 |
| p |
| 2 |
| 1 |
| 2 |
| ||
| 2p |
| p |
| 2 |
S△BB'F=
| 1 |
| 2 |
| 1 |
| 2 |
| p |
| 2 |
| 1 |
| 2 |
| ||
| 2p |
| p |
| 2 |
∴
| 1 |
| 2 |
| ||
| 2p |
| p |
| 2 |
| 1 |
| 2 |
| ||
| 2p |
| p |
| 2 |
| p2 |
| 4 |
| p2 |
| 2 |
| ||
| 4 |
| ||
| 4 |
| p4 |
| 4 |
S△A′B′F=
| p |
| 2 |
| m2+1 |
∵四边形AA′B′F与BB′A′F的面积分别为15和7
∴
| p4 |
| 4 |
∴
| 1 |
| 4 |
∴
| 3 |
| 4 |
∴S=6
故答案为:6
点评:本题考查抛物线的性质,考查面积的计算,解题的关键是正确求出三角形的面积,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
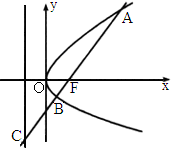
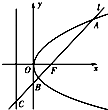 如图所示,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线l′点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( )
如图所示,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线l′点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( )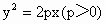 的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为
的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为
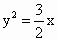
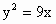
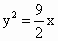
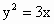
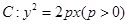 的焦点F作直线交C于A、B两点,过A、B分别向C的准线
的焦点F作直线交C于A、B两点,过A、B分别向C的准线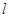 作垂线,垂足为
作垂线,垂足为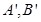 ,已知四边形
,已知四边形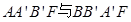 的面积分别为15和7,则
的面积分别为15和7,则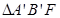 的面积为
。
的面积为
。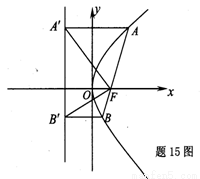
 如图所示,过抛物线C:y2=2px(p>0)的焦点F作直线交C于A、B两点,过A、B分别向C的准线l作垂线,垂足为A′,B′,已知四边形AA′B′F与BB′A′F的面积分别为15和7,则△A′B′F的面积为________.
如图所示,过抛物线C:y2=2px(p>0)的焦点F作直线交C于A、B两点,过A、B分别向C的准线l作垂线,垂足为A′,B′,已知四边形AA′B′F与BB′A′F的面积分别为15和7,则△A′B′F的面积为________.