题目内容
对于一个函数f(x),如果对任意一个三角形,只要它的三边长a,b,c都在f(x)的定义域内,就有f(a),f(b),f(c)也是某个三角形的三边长,则称f(x)为“保三角形函数”.则下列函数:①f(x)=x②f(x)=x2③f(x)=sinx,x∈(0,
)④f(x)=cosx,x∈(0,
)是“保三角形函数”的是
| π |
| 4 |
| π |
| 4 |
①③④
①③④
(写出正确的序号)分析:欲判断三个函数f(x)是不是“保三角形函数”,只须任给三角形,设它的三边长分别为a,b,c,则a+b>c,不妨假设a≤c,b≤c,我们判断f(a),f(b),f(c)是否满足任意两数之和大于第三个数,即任意两边之和大于第三边即可.
解答:解:任给三角形,设它的三边长分别为a,b,c,则a+b>c,不妨假设a≤c,b≤c,
若f(x)=x由于f(a)+f(b)=a+b>c=f(c),所以f(x)=x是“保三角形函数”.
对于f(x)=x2,3,3,5可作为一个三角形的三边长,但32+32<52,
所以不存在三角形以32,32,52为三边长,故f3(x)不是“保三角形函数”.
对于f(x)=sinx,x∈(0,
),∴
>a+b>c>0,f(a)+f(b)=sina+sinb>sinc=f(c)
所以f(x)=sinx,x∈(0,
)是“保三角形函数”.
对于f(x)=cosx,x∈(0,
),a≤c,b≤c,cosb>cosc∴f(a)+f(b)=cosa+cosb>cosc=f(c)
所以f(x)=cosx,x∈(0,
)是“保三角形函数”.
故答案为:①③④
若f(x)=x由于f(a)+f(b)=a+b>c=f(c),所以f(x)=x是“保三角形函数”.
对于f(x)=x2,3,3,5可作为一个三角形的三边长,但32+32<52,
所以不存在三角形以32,32,52为三边长,故f3(x)不是“保三角形函数”.
对于f(x)=sinx,x∈(0,
| π |
| 4 |
| π |
| 2 |
所以f(x)=sinx,x∈(0,
| π |
| 4 |
对于f(x)=cosx,x∈(0,
| π |
| 4 |
所以f(x)=cosx,x∈(0,
| π |
| 4 |
故答案为:①③④
点评:要想判断f(x)为“保三角形函数”,要经过严密的论证说明f(x)满足“保三角形函数”的概念,但要判断f(x)不为“保三角形函数”,仅须要举出一个反例即可.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 ,③f(x)=
,③f(x)= ,④f(x)=x2,⑤f(x)=e-x,
,④f(x)=x2,⑤f(x)=e-x,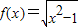 ,④f(x)=x2,其中在[1,+∞)有一个宽度为1的通道的函数的序号是 .
,④f(x)=x2,其中在[1,+∞)有一个宽度为1的通道的函数的序号是 .