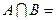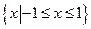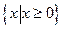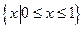题目内容
(14分)已知集合A={x|x2-2x-8≤0,x∈R},B={x|x2-(2m-3)x+m2-3m≤0,x∈R,m∈R }.
(1)若A∩B=[2,4],求实数m的值;
(2)设全集为R,若A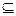 ∁RB,求实数m的取值范围.
∁RB,求实数m的取值范围.
(1)若A∩B=[2,4],求实数m的值;
(2)设全集为R,若A
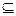 ∁RB,求实数m的取值范围.
∁RB,求实数m的取值范围.解:由已知得A=[-2,4],B=[m-3,m].
(1)∵A∩B=[2,4],∴∴m=5.
(2)∵B=[m-3,m],∴∁RB=(-∞,m-3)∪(m,+∞).∵A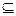 ∁RB,
∁RB,
∴m-3>4或m<-2.∴m>7或m<-2.∴m∈(-∞,-2)∪(7,+∞).
(1)∵A∩B=[2,4],∴∴m=5.
(2)∵B=[m-3,m],∴∁RB=(-∞,m-3)∪(m,+∞).∵A
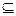 ∁RB,
∁RB,∴m-3>4或m<-2.∴m>7或m<-2.∴m∈(-∞,-2)∪(7,+∞).
略

练习册系列答案
相关题目
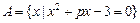 ,集合
,集合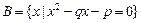 ,且
,且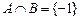 ,求
,求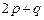 的值.
的值.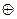 为:A1
为:A1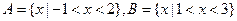 ,那么
,那么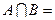 ( )
( )
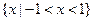
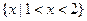
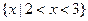
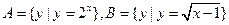 ,则
,则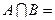 ▲ .
▲ .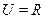 ,
,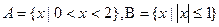 ,则
,则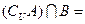 ( )
( )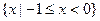
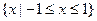
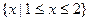
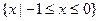
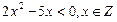 },若P∩Q ≠
},若P∩Q ≠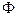 ,则m等于 ( )
,则m等于 ( ) 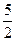
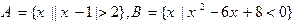 ,则
,则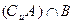 =( )
=( )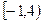
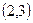
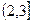
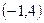
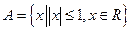 ,
,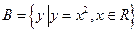 ,则
,则