题目内容
(I)求函数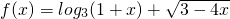 的定义域;
的定义域;
(2)判断并证明函数f(x)= 的奇偶性
的奇偶性
(3)证明函数 f(x)= 在x∈[2,+∞)上是增函数,并求f(x)在[4,8]上的值域.
在x∈[2,+∞)上是增函数,并求f(x)在[4,8]上的值域.
解:(Ⅰ)由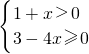 得-1<x≤
得-1<x≤ ,
,
∴求函数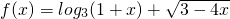 的定义域为:{ x|-1<x≤
的定义域为:{ x|-1<x≤ }
}
(2)f(x)=x+ 为奇函数
为奇函数
证明:∵f(-x)=-x- =-(x+
=-(x+ )=-f(x),
)=-f(x),
∴f(x)=x+ 为奇函数.
为奇函数.
(3)证明:设2<x1<x2,
f(x1)-f(x2)=x1+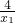 -x2-
-x2-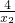
=x1-x2-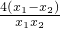
=(x1-x2)(1-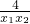 )
)
∵2<x1<x2,
∴x1-x2<0,x1x2>4,即0<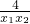 <1.
<1.
∴1-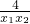 >0,
>0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2);
∴f(x)是增函数.
由(1)知f(x)在[4,8]上是增函数
∴f(x)max=f(8)= ,f(x)min=f(4)=5.
,f(x)min=f(4)=5.
∴f(x)在[4,8]上的值域为[5, ].
].
分析:(1)由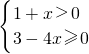 可求得其定义域;
可求得其定义域;
(2)由奇函数的定义f(-x)=-x- =-(x+
=-(x+ )=-f(x),可判断f(x)为奇函数;
)=-f(x),可判断f(x)为奇函数;
(3)利用单调函数的定义,设2<x1<x2,作差f(x1)-f(x2)化积判断符号即可.
点评:本题考查奇偶性与单调性的综合,着重考查函数的奇偶性与单调性的定义及其应用,突出转化思想的运用,属于中档题.
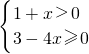 得-1<x≤
得-1<x≤ ,
,∴求函数
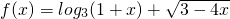 的定义域为:{ x|-1<x≤
的定义域为:{ x|-1<x≤ }
}(2)f(x)=x+
 为奇函数
为奇函数证明:∵f(-x)=-x-
 =-(x+
=-(x+ )=-f(x),
)=-f(x),∴f(x)=x+
 为奇函数.
为奇函数.(3)证明:设2<x1<x2,
f(x1)-f(x2)=x1+
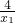 -x2-
-x2-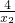
=x1-x2-
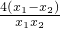
=(x1-x2)(1-
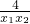 )
)∵2<x1<x2,
∴x1-x2<0,x1x2>4,即0<
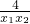 <1.
<1.∴1-
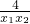 >0,
>0,∴f(x1)-f(x2)<0,即f(x1)<f(x2);
∴f(x)是增函数.
由(1)知f(x)在[4,8]上是增函数
∴f(x)max=f(8)=
 ,f(x)min=f(4)=5.
,f(x)min=f(4)=5.∴f(x)在[4,8]上的值域为[5,
 ].
].分析:(1)由
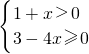 可求得其定义域;
可求得其定义域;(2)由奇函数的定义f(-x)=-x-
 =-(x+
=-(x+ )=-f(x),可判断f(x)为奇函数;
)=-f(x),可判断f(x)为奇函数;(3)利用单调函数的定义,设2<x1<x2,作差f(x1)-f(x2)化积判断符号即可.
点评:本题考查奇偶性与单调性的综合,着重考查函数的奇偶性与单调性的定义及其应用,突出转化思想的运用,属于中档题.

练习册系列答案
相关题目
 ,
, ,若函数
,若函数
 的定义域;
的定义域; ,
, ,若函数
,若函数
 的定义域;
的定义域;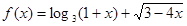 的定义域;
的定义域;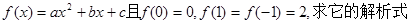 ,判断并证明该函数的奇偶性;
,判断并证明该函数的奇偶性; 的定义域;
的定义域; 的奇偶性
的奇偶性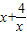 在x∈[2,+∞)上是增函数,并求f(x)在[4,8]上的值域.
在x∈[2,+∞)上是增函数,并求f(x)在[4,8]上的值域.