Question

设Q为平面上以A（5，2），B（1，1），C（1，5）三点为顶点的三角形区域（包括三角形的内部及边界）
（1）请你用不等式组表示该平面区域Q；
（2）当点（x，y）在区域Q上变动时，求：Z=x+2y的最大值和最小值．

Answer 1

分析：（1）处理的思路为：根据已知的可行域，给出对应的约束条件，处理的方法遵循“线定界，点定域”，
（2）再使用角点法，求出目标函数的最大值即可．

解答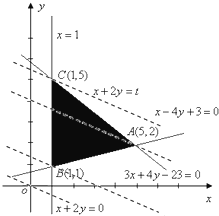：解：（1）直线AB的方程是x-4y+3=0
直线BC是方程x=1
直线AC是方程3x+4y-23=0
从而所求不等式组为

x-4y+3≤0 3x+4y-23≤0 x≥1

…（6分）
（2）如图所示，
①作直线L；x+2y=0，
②作一组平行于l的直线
l'：x+2y=t，
③观察可知
l′过点C时，Z=x+2y的值最大，
最大值为11；
④l′过点B时，Z=x+2y的值最小，最小值为3．
因此，Z=x+2y的最大值11，最小值为3．…（12分）

点评：用图解法解决线性规划问题时，分析题目的已知条件，找出约束条件和目标函数是关键，可先将题目中的量分类、列出表格，理清头绪，然后列出不等式组（方程组）寻求约束条件，并就题目所述找出目标函数．然后将可行域各角点的值一一代入，最后比较，即可得到目标函数的最优解．