题目内容

对于每一个实数x，f（x）取4-x，x+2，3x三个值中最小的值，则f（x）的最大值为
 
．
分析：画出函数y=4-x，y=x+2，y=3x的图象，结合图象，得出答案．
解答：解；画出函数y=4-x，y=x+2，y=3x的图象，如图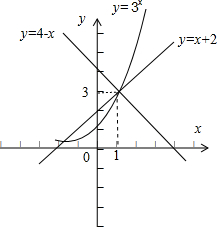，精英家教网；
f（x）=min{4-x，x+2，3x}=
x+2…x≤x0
3x…．x0＜x≤1
4-x…x＞1
，
∴f（x）的最大值为f（1）=3；
故答案为：3．
点评：本题考查了几个函数组成的新函数的最值问题，结合图象，容易得出答案．
练习册系列答案
相关题目
9、对于每一个实数x，f（x）是2-x与x中的较小者，则函数f（x）的值域是
（-∞，1]
．
对于每一个实数x，f（x）是y=2x与y=-x+1这两个函数中的较小者，则f（x）的最大值（　　）
下列命题中
①对于每一个实数x，f（x）是y=2-x2和y=x这两个函数中的较小者，则f（x）的最大值是1．
②已知x1是方程x+lgx=3的根，x2是方程x+10x=3的根，则x1+x2=3．
③函数f（x）=ax2+bx+3a+b是偶函数，其定义域为[a-1，2a]，则f（x）的图象是以（0，1）为顶点，开口向下的抛物线．
④若集合P={x|x=3m+1，m∈N+}，Q={x|x=5n+2，n∈N+}，则P∩Q={x|x=15m-8，m∈N+}
⑤若函数f（x）在（-∞，+∞）上递增，且a+b≥0，则f（a）+f（b）≥f（-a）+f（-b）．
其中正确的命题的序号是
①②④⑤
①②④⑤
．
下列命题中
①对于每一个实数x，f（x）是y=2-x2和y=x这两个函数中的较小者，则f（x）的最大值是1．
②已知x1是方程x+lgx=3的根，x2是方程x+10x=3的根，则x1+x2=3．
③函数f（x）=ax2+bx+3a+b是偶函数，其定义域为[a-1，2a]，则f（x）的图象是以（0，1）为顶点，开口向下的抛物线．
④若集合P={x|x=3m+1，m∈N+}，Q={x|x=5n+2，n∈N+}，则P∩Q={x|x=15m-8，m∈N+}
⑤若函数f（x）在（-∞，+∞）上递增，且a+b≥0，则f（a）+f（b）≥f（-a）+f（-b）．
其中正确的命题的序号是    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网