题目内容
如图,顶点在坐标原点,开口向上的抛物线经过A0(1,1),过A0作抛物线的切线交x轴于B1,过B1点作x轴的垂线交抛物线于A1,过A1作抛物线的切线交x轴于B2,……,过An(xn,yn)作抛物线的切线交x轴于
Bn+1(xn+1,0),
(1)求{xn},{yn}的通项公式;
(2)设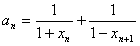 ,数列{an}的前n项和为Tn,求证:Tn>2n-
,数列{an}的前n项和为Tn,求证:Tn>2n-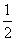 ;
;
(3)设bn=1-log2yn,若对任意正整数n,不等式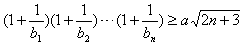 成立,求正数a的取值范围.
成立,求正数a的取值范围.
Bn+1(xn+1,0),
(1)求{xn},{yn}的通项公式;
(2)设
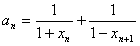 ,数列{an}的前n项和为Tn,求证:Tn>2n-
,数列{an}的前n项和为Tn,求证:Tn>2n-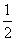 ;
;(3)设bn=1-log2yn,若对任意正整数n,不等式
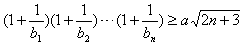 成立,求正数a的取值范围.
成立,求正数a的取值范围.
解:(1)由已知得抛物线方程为y=x2,y′=2x,
则设过点An(xn,yn)的切线方程为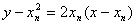 ,
,
令y=0,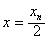 ,故
,故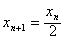 ,
,
又x0=1,
∴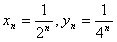 。
。
(2)由(1)知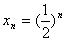 ,
,
所以
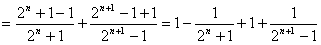
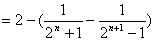 ,
,
由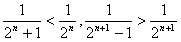 得
得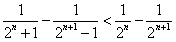 ,
,
所以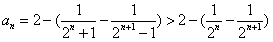 ,
,
从而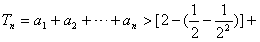
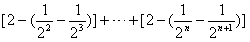
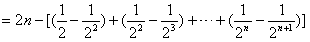
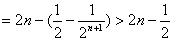 ,
,
即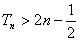 ;
;
(3)由于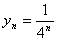 ,故bn=2n+1,
,故bn=2n+1,
对任意正整数n,不等式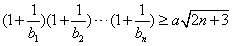 成立,
成立,
即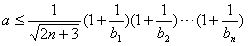 恒成立,
恒成立,
设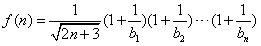 ,
,
∴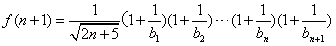 ,
,
∴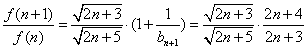
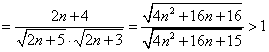 ,
,
∴f(n+1)>f(n),故f(n)递增,
∴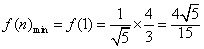 ,
,
∴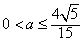 。
。
则设过点An(xn,yn)的切线方程为
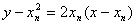 ,
,令y=0,
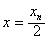 ,故
,故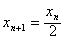 ,
,又x0=1,
∴
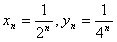 。
。(2)由(1)知
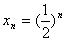 ,
,所以

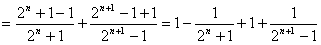
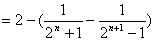 ,
,由
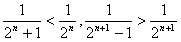 得
得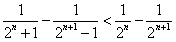 ,
,所以
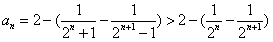 ,
,从而
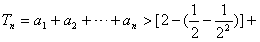
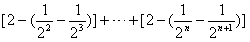
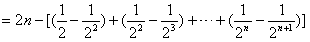
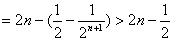 ,
,即
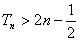 ;
;(3)由于
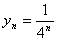 ,故bn=2n+1,
,故bn=2n+1,对任意正整数n,不等式
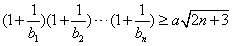 成立,
成立,即
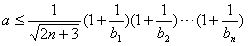 恒成立,
恒成立,设
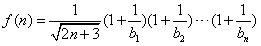 ,
,∴
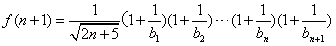 ,
,∴
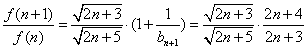
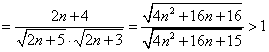 ,
,∴f(n+1)>f(n),故f(n)递增,
∴
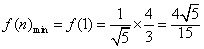 ,
,∴
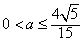 。
。
练习册系列答案
相关题目
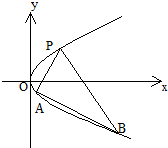 如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.
如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.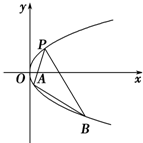 如图所示,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.当PA与PB的斜率存在且倾斜角互补时,直线AB的斜率为定值.这个定值为
如图所示,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.当PA与PB的斜率存在且倾斜角互补时,直线AB的斜率为定值.这个定值为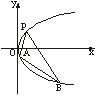
 如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.
如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(x1,y1),B(x2,y2)均在抛物线上.