题目内容
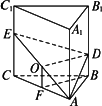
如图所示,ABC-A1B1C1为正三棱柱,底面边长为a,D、E分别是BB1、CC1上的点且EC=2BD=a,求证:平面ADE⊥平面ACC1A1.
答案:
解析:
提示:
解析:
证明:取AE的中点O,AC的中点F,连结OF、BF、OD,由条件计算AD=![]() a,∵四边形BDEC为直角梯形,且EC=2BD=a,∴DE=
a,∵四边形BDEC为直角梯形,且EC=2BD=a,∴DE=![]() a,∴DAE为等腰三角形,∴DO⊥AE.
a,∴DAE为等腰三角形,∴DO⊥AE.
又OF∥EC且OF=![]() EC=a,∴OF∥BD且OF=BD,OF⊥BF,
EC=a,∴OF∥BD且OF=BD,OF⊥BF,
∴四边形BDOF是矩形,
∴DO⊥OF.
又OF∩AE=O,∴DO⊥平面AA1C1C.
又DO![]() 平面ADE,
平面ADE,
∴平面ADE⊥平面AA1C1C.
提示:
本题的关键在于证明DO⊥平面ACC1A1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,△ABC和△A'B'C'是在各边的
如图所示,△ABC和△A'B'C'是在各边的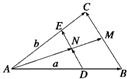 如图所示,△ABC中,
如图所示,△ABC中,
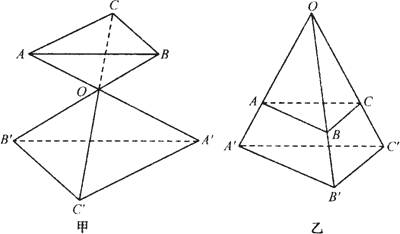
 处相交的两个正三角形,△ABC的边长为a,图中列出了长度均为
处相交的两个正三角形,△ABC的边长为a,图中列出了长度均为 的若干个向量,则
的若干个向量,则 相等的向量是 ;
相等的向量是 ; 平行的向量是 .
平行的向量是 .