题目内容
满足条件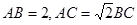 的△
的△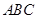 的面积的最大值为 .
的面积的最大值为 .
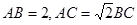 的△
的△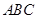 的面积的最大值为 .
的面积的最大值为 .
解:设BC=x,则AC=  x,
x,
根据面积公式得S△ABC="1" /2 AB•BCsinB
="1/" 2 ×2x ,
,
根据余弦定理得cosB=(AB2+BC2-AC2)/2AB•BC=[4+x2-( x)2] /4x =(4-x2) /4x ,
x)2] /4x =(4-x2) /4x ,
代入上式得
S△ABC=x
由三角形三边关系有 x+x>2
x+x>2
x+2> x ,
x ,
解得2 -2<x<2
-2<x<2 +2.
+2.
故当x=2 时,S△ABC取得最大值2
时,S△ABC取得最大值2
 x,
x,根据面积公式得S△ABC="1" /2 AB•BCsinB
="1/" 2 ×2x
 ,
,根据余弦定理得cosB=(AB2+BC2-AC2)/2AB•BC=[4+x2-(
 x)2] /4x =(4-x2) /4x ,
x)2] /4x =(4-x2) /4x ,代入上式得
S△ABC=x

由三角形三边关系有
 x+x>2
x+x>2 x+2>
 x ,
x ,解得2
 -2<x<2
-2<x<2 +2.
+2.故当x=2
 时,S△ABC取得最大值2
时,S△ABC取得最大值2

练习册系列答案
相关题目
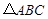 中,
中,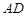 为
为 边上的中线,
边上的中线,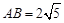 ,
,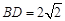 ,
,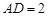 ,则
,则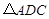 的面积
的面积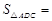 .
.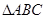 中,已知
中,已知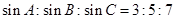 ,则此三角形的最大内角为( )
,则此三角形的最大内角为( )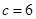 ,∠A=30°,∠B=120°,则△ABC的面积为___
,∠A=30°,∠B=120°,则△ABC的面积为___ 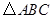 中,
中,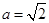 ,
,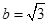 ,
,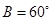 ,那么角
,那么角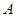 等于
等于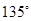
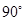
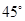
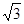 ,AC=2,则△ABC的面积是______。
,AC=2,则△ABC的面积是______。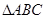 中,已知
中,已知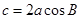 ,则
,则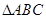 中,若
中,若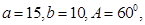 则
则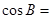 ( )
( )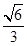

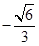
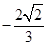
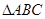 中,边
中,边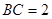 ,
,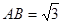 ,则角
,则角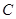 的取值范围是 .
的取值范围是 .