题目内容
某地区举行环保知识大赛,比赛分初赛和决赛两部分,初赛采用选用选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题直接进入决赛,答错3次者则被淘汰,已知选手甲连续两次答错的概率为| 1 | 9 |
(I)求甲选手回答一个问题的正确率;
(II)求选手甲进入决赛的概率;
(III)设选手甲在初赛中的答题的个数为ξ,试求ξ的分布列,并求出ξ的数学期望.
分析:(I)甲答对一个问题的正确率为P1由题意,(1-P 1)2=
,解方程求出正答率
(II)由题意进入决赛至少答对三道题,故进行决赛分为三类事件,答对三题入决赛,四题入决赛,五题入决赛,分别算出这三个事件的概率,求其和即可;
(III)ξ的取值为3,4,5,对应的事件分别是前三个题全部答对,前四个题答对了三个,其中第四题一定对,前五个题答对了三个,第五个一定答对,分别求出它们的概率,列出分布列,求出期望.
| 1 |
| 9 |
(II)由题意进入决赛至少答对三道题,故进行决赛分为三类事件,答对三题入决赛,四题入决赛,五题入决赛,分别算出这三个事件的概率,求其和即可;
(III)ξ的取值为3,4,5,对应的事件分别是前三个题全部答对,前四个题答对了三个,其中第四题一定对,前五个题答对了三个,第五个一定答对,分别求出它们的概率,列出分布列,求出期望.
解答:解:(I)设甲答对一个问题的正确率为P1
由题意:(1-P)2=
?P=
所以,甲答对一个问题的正确率为
…(3分)
(II)甲答了3道题进入决赛的概率为(
)3=
甲答了4道题进入决赛的概率为
(
)2(
)=
甲答了5道题进入决赛的概率为
(
)3(
)2=
故选手甲进入决赛的概率为
+
+
=
所以,选手甲进入决赛的概率为
.…(7分)
(III)ξ的取值为3,4,5,其中
P(ξ=4)=
(
)3(
)+
(
)2•
•
=
P(ξ=5)=
(
)2(
)2=
P(ξ=3)=1-
-
=
所以,ξ的分布列为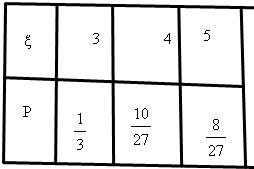
其数学期望为Eξ=3×
+4×
+5×
=
由题意:(1-P)2=
| 1 |
| 9 |
| 2 |
| 3 |
所以,甲答对一个问题的正确率为
| 2 |
| 3 |
(II)甲答了3道题进入决赛的概率为(
| 2 |
| 3 |
| 8 |
| 27 |
甲答了4道题进入决赛的概率为
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 27 |
甲答了5道题进入决赛的概率为
| C | 2 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 16 |
| 81 |
故选手甲进入决赛的概率为
| 8 |
| 27 |
| 8 |
| 27 |
| 16 |
| 81 |
| 64 |
| 81 |
所以,选手甲进入决赛的概率为
| 64 |
| 81 |
(III)ξ的取值为3,4,5,其中
P(ξ=4)=
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| C | 2 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 10 |
| 27 |
P(ξ=5)=
| C | 2 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 27 |
P(ξ=3)=1-
| 8 |
| 27 |
| 10 |
| 27 |
| 1 |
| 3 |
所以,ξ的分布列为

其数学期望为Eξ=3×
| 1 |
| 3 |
| 10 |
| 27 |
| 8 |
| 27 |
| 107 |
| 27 |
点评:本题考查离散型随机变量的分布列与期望,解题的关键是根据概率公式求出分布列,再由求期望的公式求出期望.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 (已知甲回答每个问题的正确率相同,且相互之间没有影响)
(已知甲回答每个问题的正确率相同,且相互之间没有影响) (已知甲回答每个问题的正确率相同,且相互之间没有影响)
(已知甲回答每个问题的正确率相同,且相互之间没有影响) (已知甲回答每个问题的正确率相同,且相互之间没有影响)
(已知甲回答每个问题的正确率相同,且相互之间没有影响)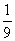 (已知甲回答每个问题的正确率相同,且相互之间没有影响)
(已知甲回答每个问题的正确率相同,且相互之间没有影响)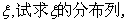 并求出
并求出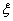 的数学期望。
的数学期望。