题目内容
设0＜x＜π，则函数y=
的最小值是（ ）
| 2-cosx |
| sinx |
| A、3 | ||
| B、2 | ||
C、
| ||
D、2-
|
分析：由题意函数的最小值，转化为两点（0，2），（-sinx，cosx）的斜率的取值范围，求出最小值即可．
解答：解：0＜x＜π，则函数y=
的最小值，就是两点（0，2），（-sinx，cosx）的斜率的取值范围的最小值，画出图象：
显然（-sinx，cosx）表示动点轨迹，是以原点为圆心1为半径的y轴的左侧部分，
两点（0，2），（-sinx，cosx）的斜率的取值范围：[
，+∞）
设0＜x＜π，则函数y=
的最小值是
．
故选C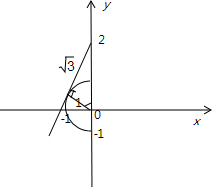
| 2-cosx |
| sinx |
显然（-sinx，cosx）表示动点轨迹，是以原点为圆心1为半径的y轴的左侧部分，
两点（0，2），（-sinx，cosx）的斜率的取值范围：[
| 3 |
设0＜x＜π，则函数y=
| 2-cosx |
| sinx |
| 3 |
故选C
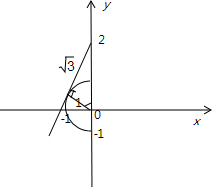
点评：本题是基础题，考查数形结合的思想，转化思想，直线的斜率的求法，考查计算能力．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
的最小值是________．