题目内容
过点P(2,3)且以
=(1,3)为方向向量的直线l的方程为
| a |
3x-y-3=0
3x-y-3=0
.分析:若直线与x轴不垂直,则直线的一个方向向量为
=(1,k),其中k是直线的斜率.可以用向量
与已知方向向量平行,建立关系式得到直线的斜率,得到直线的点斜式方程,最后化成直线的一般式方程即可.
| a |
| a |
解答:解:设直线l的另一个方向向量为
=(1,k),其中k是直线的斜率
可得
=(1,3)与
=(1,k)互相平行
∴
=
⇒k=3,
所以直线l的点斜式方程为:y-3=3(x-2)
化成一般式:3x-y-3=0
故答案为:3x-y-3=0.
| a |
可得
| a |
| a |
∴
| 1 |
| 1 |
| k |
| 3 |
所以直线l的点斜式方程为:y-3=3(x-2)
化成一般式:3x-y-3=0
故答案为:3x-y-3=0.
点评:本题考查了直线的方向向量,属于基础题.方向向量是与直线平行或在直线上的非零向量,如果直线的斜率存在,则它的一个方向向量为
=(1,k),其中k是直线的斜率.
| a |

练习册系列答案
相关题目
 =(2,-6)为方向向量的直线l的截距式方程为________.
=(2,-6)为方向向量的直线l的截距式方程为________.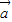 =(2,-6)为方向向量的直线l的截距式方程为 .
=(2,-6)为方向向量的直线l的截距式方程为 .