题目内容
下列命题中,其“非”是真命题的是( )A.对任意x∈R,x2-2
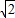 x+2≥0;
x+2≥0;B.存在x∈R,使x3-x2+1=0;
C.存在n∈N+,使点P(n,n2-2)在直线y=2x+1上;
D.对任意a,b∈R,方程ax=b都有唯一解
【答案】分析:根据二次函数的图象和性质可判断A中原命题为真,则其“非”是假命题;
根据三次函数的图象和性质可判断B中原命题为真,则其“非”是假命题;
令n=3可判断C中原命题为真,则其“非”是假命题;
分别令a=0,b=0和a=0,b≠0可判断D中原命题为假,则其“非”是真命题;
解答:解:∵△=8-8=0,故命题任意x∈R,x2-2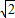 x+2≥0为真,则其“非”是假命题;
x+2≥0为真,则其“非”是假命题;
∵函数y=x3-x2+1的值域为R,且图象是连续的,故存在x∈R,使x3-x2+1=0为真,则其“非”是假命题;
当n=3,使点P(n,n2-2)即(3,7)点在直线y=2x+1上,故存在n∈N+,使点P(n,n2-2)在直线y=2x+1上为真,则其“非”是假命题;
当a=0,b=0时,方程ax=b有无数个解,当a=0,b≠0时,方程ax=b无解,故对任意a,b∈R,方程ax=b都有唯一解为假,则其“非”是真命题;
故选D
点评:本题以命题真假判断为载体考查了二次函数的图象和性质,二次不等式恒成立问题,三次函数的图象和性质,类一次方程的解等知识点,是函数、不等式、方程的一个简单综合应用,难度不大.
根据三次函数的图象和性质可判断B中原命题为真,则其“非”是假命题;
令n=3可判断C中原命题为真,则其“非”是假命题;
分别令a=0,b=0和a=0,b≠0可判断D中原命题为假,则其“非”是真命题;
解答:解:∵△=8-8=0,故命题任意x∈R,x2-2
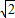 x+2≥0为真,则其“非”是假命题;
x+2≥0为真,则其“非”是假命题;∵函数y=x3-x2+1的值域为R,且图象是连续的,故存在x∈R,使x3-x2+1=0为真,则其“非”是假命题;
当n=3,使点P(n,n2-2)即(3,7)点在直线y=2x+1上,故存在n∈N+,使点P(n,n2-2)在直线y=2x+1上为真,则其“非”是假命题;
当a=0,b=0时,方程ax=b有无数个解,当a=0,b≠0时,方程ax=b无解,故对任意a,b∈R,方程ax=b都有唯一解为假,则其“非”是真命题;
故选D
点评:本题以命题真假判断为载体考查了二次函数的图象和性质,二次不等式恒成立问题,三次函数的图象和性质,类一次方程的解等知识点,是函数、不等式、方程的一个简单综合应用,难度不大.

练习册系列答案
相关题目
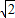 x+2≥0;
x+2≥0;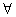 x∈R ,x2-2x+2≥0
x∈R ,x2-2x+2≥0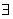 x∈R,3x-5=0
x∈R,3x-5=0