题目内容
圆x2+y2+2x=0和x2+y2﹣4y=0的公共弦所在直线方程为( )
| A.x﹣2y=0 | B.x+2y=0 | C.2x﹣y=0 | D.2x+y=0 |
B
解析

练习册系列答案
相关题目
设直线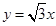 与圆
与圆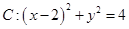 交于
交于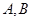 两点,则弦长
两点,则弦长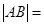 ( )
( )
A.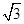 | B.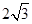 | C.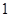 | D.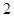 |
已知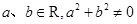 ,则直线
,则直线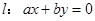 与圆:
与圆: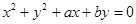 的位置关系是( ).
的位置关系是( ).
| A.相交 | B.相切 | C.相离 | D.不能确定 |
直线y=x+b与曲线x=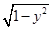 有且仅有一个公共点,则b的取值范围是( )
有且仅有一个公共点,则b的取值范围是( )
A.{b|b=± } } |
B.{b|-1<b≤1或b=- } } |
C.{b|-1≤b≤ } } |
D.{b|- <b<1} <b<1} |
经过圆x2+2x+y2=0的圆心C,且与直线x+y=0垂直的直线方程是( )
| A.x+y+1=0 | B.x+y﹣1=0 |
| C.x﹣y+1=0 | D.x﹣y﹣1=0 |
曲线f(x)=xlnx在点P(1,0)处的切线l与坐标轴围成的三角形的外接圆方程是( )
A.(x+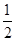 )2+(y- )2+(y-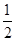 )2= )2=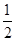 |
B.(x+1)2+(y-1)2=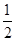 |
C.(x-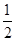 )2+(y+ )2+(y+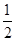 )2= )2=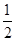 |
D.(x-1)2+(y+1)2=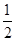 |
设圆 的一条切线与
的一条切线与 轴、
轴、 轴分别交于点
轴分别交于点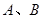 , 则
, 则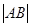 的最小值为( )
的最小值为( )
| A.4 | B.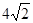 | C.6 | D.8 |
若直线2x-y+a=0与圆(x-1)2+y2=1有公共点,则实数a的取值范围是( )
A.-2-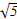 <a<-2+ <a<-2+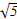 |
B.-2-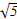 ≤a≤-2+ ≤a≤-2+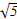 |
C.-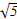 ≤a≤ ≤a≤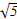 |
D.-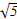 <a< <a<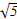 |
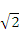 ,0)引直线ι与曲线
,0)引直线ι与曲线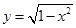 交于A,B两点 ,O为坐标原点,当△AOB的面积取最大值时,直线ι的斜率等于( )
交于A,B两点 ,O为坐标原点,当△AOB的面积取最大值时,直线ι的斜率等于( )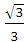 B.-
B.-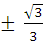 D-
D-