题目内容
设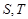 是
是 的两个非空子集,如果存在一个从
的两个非空子集,如果存在一个从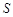 到
到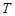 的函数
的函数 满足:
满足:
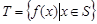 ;
;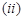 对任意
对任意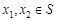 ,当
,当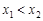 时,恒有
时,恒有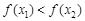 ,那么称这两个集合“保序同构”,以下集合对不是“保序同构”的是( )
,那么称这两个集合“保序同构”,以下集合对不是“保序同构”的是( )
A. | B.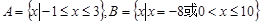 |
C.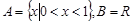 | D.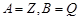 |
D
解析

练习册系列答案
相关题目
设集合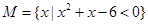 ,
,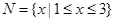 ,则
,则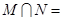 ( )
( )
A.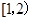 | B.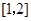 | C.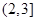 | D.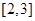 |
设集合 ,
, ,
,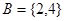 ,则图中阴影( )部分所表示的集合是
,则图中阴影( )部分所表示的集合是 
A.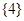 | B. | C.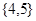 | D.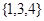 |
已知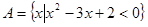 ,
,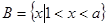 ,若
,若 ,则实数
,则实数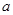 的取值范围是
的取值范围是
A. | B.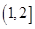 | C.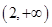 | D.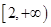 |
设全集U={1,2,3,4,5},集合A={1,2},B={2,3},则A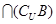 =
=
| A.{4,5} | B.{2,3} | C.{1} | D.{3} |
已知全集 ,集合
,集合 ,则
,则
A. | B.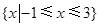 |
C.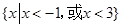 | D. |
已知 为全集,
为全集, ,则
,则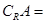
A. | B.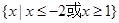 |
C.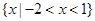 | D. |
已知集合 ,
,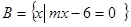 ,若
,若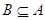 ,实数
,实数 =( )
=( )
| A.3 | B.2 | C.2或3 | D.0或2或3 |
设集合 ={
={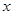 |
| },
}, ={
={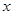 |
| }.则
}.则 =
=
A.{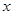 |-7< |-7<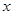 <-5 } <-5 } | B.{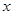 | 3< | 3<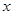 <5 } <5 } |
C.{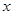 | -5 < | -5 <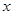 <3} <3} | D.{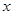 | -7< | -7<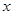 <5 } <5 } |