题目内容
为测量某塔AB的高度,在一幢与塔AB相距20m的楼顶处测得塔顶A的仰角为30°,测得塔基B的俯角为45°,那么塔AB的高度是
- A.20(1+
 ) m
) m - B.20(1+
 ) m
) m - C.20(1+
 )m
)m - D.30 m
C
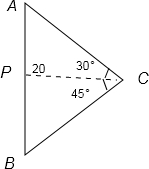
分析:如图所示:设观测点为C,CP=20m 为点C与塔AB的距离,∠ACP=30°,∠BCP=45°.利用直角三角形中的边角关系求得AP、CP的值,即可求得塔高AB的值.
解答:如图所示:设观测点为C,CP=20为点C与塔AB的距离,∠ACP=30°,∠BCP=45°.
则AB=AP+CP=PC•tan30°+CP•tan45°=20× +20×1=20(1+
+20×1=20(1+ ),故塔AB的高度是20(1+
),故塔AB的高度是20(1+ )m,
)m,
故选C.
点评:本题主要考查解三角形,直角三角形中的边角关系应用,考查基本运算,属于中档题.
分析:如图所示:设观测点为C,CP=20m 为点C与塔AB的距离,∠ACP=30°,∠BCP=45°.利用直角三角形中的边角关系求得AP、CP的值,即可求得塔高AB的值.
解答:如图所示:设观测点为C,CP=20为点C与塔AB的距离,∠ACP=30°,∠BCP=45°.
则AB=AP+CP=PC•tan30°+CP•tan45°=20×
 +20×1=20(1+
+20×1=20(1+ ),故塔AB的高度是20(1+
),故塔AB的高度是20(1+ )m,
)m,
故选C.
点评:本题主要考查解三角形,直角三角形中的边角关系应用,考查基本运算,属于中档题.

练习册系列答案
相关题目
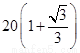 m B.
m B. 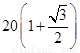 m C.
m C. 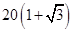 m D.30 m
m D.30 m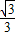 ) m
) m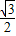 ) m
) m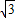 )m
)m