题目内容
(1)P={x|x2-2x-3=0},S={x|ax+2=0},S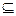 P,求a取值?
P,求a取值?
(2)A={x|-2≤x≤5} ,B={x|m+1≤x≤2m-1},B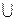 A=A,求m的范围?
A=A,求m的范围?
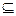 P,求a取值?
P,求a取值?(2)A={x|-2≤x≤5} ,B={x|m+1≤x≤2m-1},B
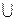 A=A,求m的范围?
A=A,求m的范围?(1)a值为0或-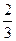 或2 (2)m≤3
或2 (2)m≤3
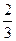 或2 (2)m≤3
或2 (2)m≤3(1)a=0,S=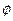 ,
,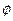
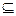 P成立 a
P成立 a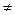 0,S
0,S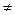
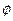 ,由S
,由S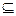 P,P={3,-1}
P,P={3,-1}
得3a+2=0,a=-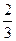 或-a+2=0,a=2; ∴a值为0或-
或-a+2=0,a=2; ∴a值为0或-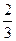 或2.
或2.
(2)因为B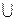 A=A,所以B
A=A,所以B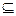 A
A
当B=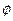 ,即m+1>2m-1,m<2
,即m+1>2m-1,m<2 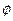
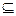 A成立.
A成立.
当 B≠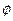 ,由题意得
,由题意得
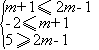 解得2≤m≤3
解得2≤m≤3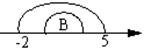
∴m<2或2≤m≤3 即m≤3为所求的取值范围.
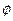 ,
,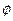
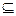 P成立 a
P成立 a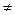 0,S
0,S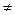
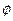 ,由S
,由S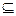 P,P={3,-1}
P,P={3,-1}得3a+2=0,a=-
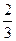 或-a+2=0,a=2; ∴a值为0或-
或-a+2=0,a=2; ∴a值为0或-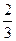 或2.
或2.(2)因为B
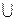 A=A,所以B
A=A,所以B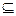 A
A当B=
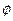 ,即m+1>2m-1,m<2
,即m+1>2m-1,m<2 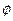
 A成立.
A成立.当 B≠
 ,由题意得
,由题意得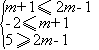 解得2≤m≤3
解得2≤m≤3
∴m<2或2≤m≤3 即m≤3为所求的取值范围.

练习册系列答案
相关题目
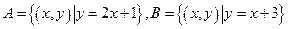
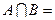
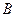
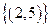
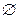
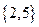
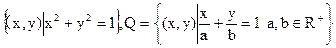 ,
,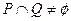 .则a、b满足( )
.则a、b满足( )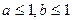 B
B 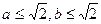 C
C 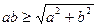
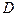
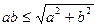
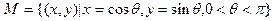 ,
,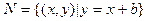 且
且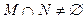 ,求b的范围。
,求b的范围。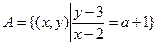 ,
,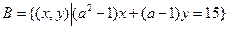 ,若
,若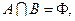 则
则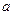 的取值是( )
的取值是( )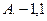
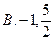
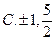
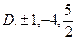
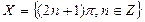 与
与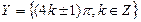 之的关系是( )
之的关系是( )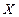

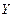 ;
;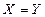 ;
;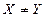
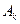 的最小元素为
的最小元素为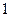 ,最大元素为
,最大元素为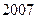 ,并且各元素可以从小到大排成一个公差为
,并且各元素可以从小到大排成一个公差为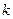 的等差数列,则并集
的等差数列,则并集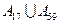 中的元素个数为( ).
中的元素个数为( ).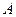 、
、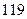
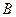 、
、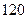 ;
; 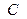 、
、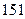 ;
; 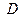 、
、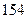 .
.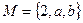 ,
,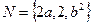 ,且
,且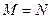 ,求
,求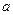 ,
,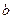 的值
的值
 ,
, ,
, ,则
,则 ( )
( )


