题目内容
过椭圆 的左焦点作直线交椭圆于A、B两点,若存在直线使坐标原点O恰好在以AB为直径的圆上,则椭圆的离心率取值范围是
的左焦点作直线交椭圆于A、B两点,若存在直线使坐标原点O恰好在以AB为直径的圆上,则椭圆的离心率取值范围是
- A.
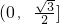
- B.
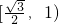
- C.
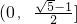
- D.
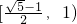
D
分析:设l:x=-c+my代入椭圆方程,设A(x1,y1),B(x2,y2),则y1,y2为整理后的方程的两个根,利用韦达定理结合OA⊥OB,可得到a,b,c之间的关系式,从而可求得椭圆的离心率取值范围.
解答:设l:x=-c+my代入椭圆方程得: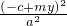 +
+ =1,
=1,
整理得:(b2m2+a2)y2-2mcb2y-b4=0,
设A(x1,y1),B(x2,y2),则y1,y2为上述方程的两个根,
∴y1+y2=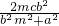 ,y1y2=-
,y1y2=-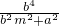 ,①
,①
∵OA⊥OB,
∴(-c+my1)(-c+my2)+y1y2=0.
∴c2-mc(y1+y2)+(m2+1)y1y2=0,将①代入,整理得:
a2c2-(c2b2+b4)m2-b4=0,
∴(c2b2+b4)m2=a2c2-b4≥0,
∴a2c2≥(a2-c2)2,又e= ,
,
∴e4-3e2+1≤0,
∴ ≤e2≤
≤e2≤ ,而0<e<1,
,而0<e<1,
∴ ≤e2<1,
≤e2<1,
∴ ≤e<1.
≤e<1.
故选D.
点评:本题考查椭圆的性质,考查直线与椭圆的位置关系,突出考查韦达定理的作用,考查垂直关系的应用,考查抽象思维与综合运算能力,属于难题.
分析:设l:x=-c+my代入椭圆方程,设A(x1,y1),B(x2,y2),则y1,y2为整理后的方程的两个根,利用韦达定理结合OA⊥OB,可得到a,b,c之间的关系式,从而可求得椭圆的离心率取值范围.
解答:设l:x=-c+my代入椭圆方程得:
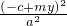 +
+ =1,
=1,整理得:(b2m2+a2)y2-2mcb2y-b4=0,
设A(x1,y1),B(x2,y2),则y1,y2为上述方程的两个根,
∴y1+y2=
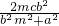 ,y1y2=-
,y1y2=-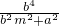 ,①
,①∵OA⊥OB,
∴(-c+my1)(-c+my2)+y1y2=0.
∴c2-mc(y1+y2)+(m2+1)y1y2=0,将①代入,整理得:
a2c2-(c2b2+b4)m2-b4=0,
∴(c2b2+b4)m2=a2c2-b4≥0,
∴a2c2≥(a2-c2)2,又e=
 ,
,∴e4-3e2+1≤0,
∴
 ≤e2≤
≤e2≤ ,而0<e<1,
,而0<e<1,∴
 ≤e2<1,
≤e2<1,∴
 ≤e<1.
≤e<1.故选D.
点评:本题考查椭圆的性质,考查直线与椭圆的位置关系,突出考查韦达定理的作用,考查垂直关系的应用,考查抽象思维与综合运算能力,属于难题.

练习册系列答案
相关题目
 的左焦点作直线交椭圆于
的左焦点作直线交椭圆于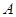 、
、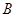 两点,若存在直线使坐标原点
两点,若存在直线使坐标原点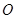 恰好在以
恰好在以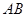 为直径的圆上,则椭圆的离心率取值范围是
为直径的圆上,则椭圆的离心率取值范围是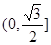 B.
B.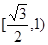 C.
C.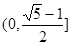 D.
D.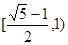
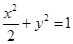 的左焦点
的左焦点 作直线
作直线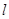 交椭圆于
交椭圆于 两点,
两点,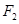 是椭圆右焦点,则
是椭圆右焦点,则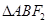 的周长为( )
的周长为( )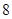 B.
B.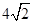 C.
C.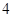 D.
D.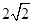
 ,且经过点
,且经过点 ,过椭圆的左焦点作直线
,过椭圆的左焦点作直线 交椭圆于A、B两点,以OA、OB为邻边作平行四边形OAPB。
交椭圆于A、B两点,以OA、OB为邻边作平行四边形OAPB。
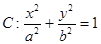 的左焦点作直线
的左焦点作直线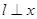 轴,交椭圆C于A,B两点,若△OAB(O为坐标原点)是直角三角形,则椭圆C的离心率e为( )
轴,交椭圆C于A,B两点,若△OAB(O为坐标原点)是直角三角形,则椭圆C的离心率e为( ) B.
B.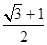 C.
C.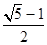 D.
D.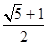
 ,点
,点 分别为椭圆的左、右焦点,过右焦点
分别为椭圆的左、右焦点,过右焦点 且垂直于长轴的弦长为
且垂直于长轴的弦长为
 作直线
作直线 ,交椭圆于
,交椭圆于 两点,若
两点,若 ,求直线
,求直线