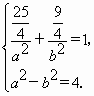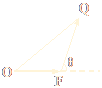题目内容
如下图,已知△OFQ的面积为S,且![]() ·
·![]() =1,
=1,

(Ⅰ)若S满足条件![]() <S<2,求向量
<S<2,求向量![]() 与
与![]() 的夹角θ的取值范围;
的夹角θ的取值范围;
(Ⅱ)设|![]() |=c(c≥2),S=
|=c(c≥2),S=![]() c,若以O为中心,F为焦点的椭圆经过点Q,当|
c,若以O为中心,F为焦点的椭圆经过点Q,当|![]() |取得最小值时,求此椭圆的方程.
|取得最小值时,求此椭圆的方程.
答案:
解析:
解析:
|
(Ⅰ)∵ 又 ∴tanθ=2S,S= 又 ∴ (Ⅱ)以
∴O(0,0),F(c,0),Q(x0,y0). 设椭圆方程为 又 ∴(c,0)·(x0-c,y0)=1.① 由①得c(x0-c)=1 由②得|y0|= ∴| ∵c≥2, ∴当c=2时,| 此时Q( 代入椭圆方程得 ∴a2=10,b2=6.∴椭圆方程为 |

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目