题目内容
在直角坐标系中，参数方程为
|
分析：将直线的参数方程与圆的极坐标方程化为普通方程联立直接可得
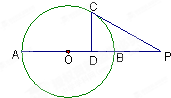
解答：解：由题意知，直线l的倾斜角为30°，
并过点A（2，0）；曲线C是以（1，0）为圆心、半径为1的圆，
且圆C也过点A（2，0）；设直线l与圆C的另一个交点为B，
在Rt△OAB中，|AB|=2cos30°=
．
故答案为
．
并过点A（2，0）；曲线C是以（1，0）为圆心、半径为1的圆，
且圆C也过点A（2，0）；设直线l与圆C的另一个交点为B，
在Rt△OAB中，|AB|=2cos30°=
| 3 |
故答案为
| 3 |
点评：直线被圆所截得的弦长可用代数和几何两种方法求解．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
选做题（在（1）（2）中任选一题，若两题都做按第（1）题计分）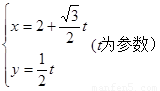
的直线
，被以原点为极点，
轴的正半轴为极轴，极坐标方程为
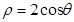的曲线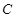
所截，求截得的弦长．
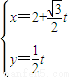（t为参数）的直线l，被以原点为极点、x轴的正半轴为极轴、极坐标方程为ρ=2cosθ的曲线C所截，则得的弦长是 ．