题目内容
设0<x<1,a,b都为大于零的常数,若
+
≥m恒成立,则m的最大值
是 ( )
| A．( a-b)2 | B．(a+b)2 |
| C．a2b2 | D．a2 |
B
解析【解题指南】本题的关键是利用x+(1-x)=1结合基本不等式加以求解.
解:选B.由+=
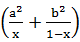[x+(1-x)]
=a2+b2+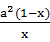
+
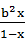
≥a2+b2+2ab=(a+b)2,
当且仅当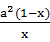=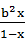时等号成立,
所以m≤(a+b)2,m的最大值为(a+b)2.
练习册系列答案
阅读快车系列答案
相关题目
若存在实数
使
成立，则实数
的取值范围是（ )..
A． | B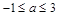． | C． | D． |
当0≤x≤
时,函数y=x2(1-5x)的最大值为 ( )
A． | B． | C． | D．无最大值 |
“a>1”是“
<1”的 ( )
| A．充分但不必要条件 | B．必要但不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
下列各函数中,最小值为2的是 ( )
A．y=x+ |
B．y= |
| C．y=logax+logxa(a>0,x>0且a≠1,x≠1) |
| D．y=3-x+3x(x>0) |
若x,y是正数,则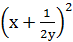
+
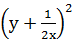的最小值是 ( )
| A．3 | B． | C．4 | D． |
设a>1>b>-1,则下列不等式中恒成立的是 ( )
A． < | B．> |
| C．a>b2 | D．a2>2b |
已知a≥0,b≥0,且a+b=2,则 ( )
A．ab≤ | B．ab≥ |
| C．a2+b2≥2 | D．a2+b2≤3 |