题目内容
给出如下三角形数表:
此数表满足:
①第n行首尾两数均为n,
②表中数字间的递推关系类似于杨辉三角,即除了“两腰”上的数字以外,每一个数都等于它上一行左右“两肩”上的两数之和.第n(n≥2)行第n-1个数是 .
【答案】分析:观察图例,我们可以得到每一行的数据都是对称的,故第n(n≥2)行第n-1个数与故第n(n≥2)行第2个数是相等的,故我们只要分析出故第n(n≥2)行第2个数取值的规律,便可得到故第n(n≥2)行第n-1个数的值与n的关系.
解答:解:由图可知:第n(n≥2)行第n-1个数等于故第n(n≥2)行第2个数
第二行的第二个数为2
第三行的第二个数为4=2+2
第四行的第二个数为7=3+2+2
第五行的第二个数为11=4+3+2+2
第六行的第二个数为16=5+4+3+2+2
…
故推断第n行的第二个数为:[(n-1)+(n-2)+…+2]+2=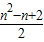
故第n(n≥2)行第n-1个数等于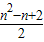
故答案为:第n(n≥2)行第n-1个数等于
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).
解答:解:由图可知:第n(n≥2)行第n-1个数等于故第n(n≥2)行第2个数
第二行的第二个数为2
第三行的第二个数为4=2+2
第四行的第二个数为7=3+2+2
第五行的第二个数为11=4+3+2+2
第六行的第二个数为16=5+4+3+2+2
…
故推断第n行的第二个数为:[(n-1)+(n-2)+…+2]+2=
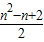
故第n(n≥2)行第n-1个数等于
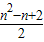
故答案为:第n(n≥2)行第n-1个数等于
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目

