题目内容
设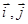 分别是
分别是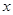 轴,
轴,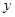 轴正方向上的单位向量,
轴正方向上的单位向量,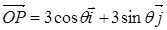 ,
,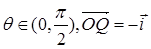 。若用α来表示
。若用α来表示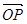 与
与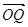 的夹角,则α等于( )
的夹角,则α等于( )
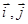 分别是
分别是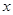 轴,
轴,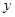 轴正方向上的单位向量,
轴正方向上的单位向量,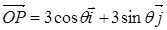 ,
,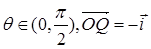 。若用α来表示
。若用α来表示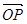 与
与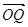 的夹角,则α等于( )
的夹角,则α等于( )A.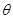 | B. | C.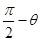 | D.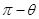 |
D
由两个向量数量积公式求得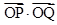 =-3cosθ,由两个向量的数量积的定义可得
=-3cosθ,由两个向量的数量积的定义可得 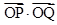 =3cosα,故有 3cosα=-3cosθ,再由θ的范围及诱导公式求出α的值.
=3cosα,故有 3cosα=-3cosθ,再由θ的范围及诱导公式求出α的值.
解:∵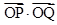 =(3cosθ
=(3cosθ +3sinθ
+3sinθ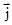 )?(-
)?(- )=-3cosθ+0=-3cosθ,
)=-3cosθ+0=-3cosθ,
由两个向量的数量积的定义可得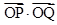 =3×1×cosα=3cosα,
=3×1×cosα=3cosα,
∴3cosα=-3cosθ,cosα=-cosθ=cos(π-θ),
∵θ∈(0,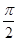 ),
),
∴π-θ∈(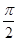 ,π),
,π),
故有 α=π-θ.
故答案为D.
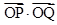 =-3cosθ,由两个向量的数量积的定义可得
=-3cosθ,由两个向量的数量积的定义可得 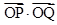 =3cosα,故有 3cosα=-3cosθ,再由θ的范围及诱导公式求出α的值.
=3cosα,故有 3cosα=-3cosθ,再由θ的范围及诱导公式求出α的值.解:∵
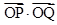 =(3cosθ
=(3cosθ +3sinθ
+3sinθ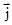 )?(-
)?(- )=-3cosθ+0=-3cosθ,
)=-3cosθ+0=-3cosθ,由两个向量的数量积的定义可得
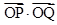 =3×1×cosα=3cosα,
=3×1×cosα=3cosα,∴3cosα=-3cosθ,cosα=-cosθ=cos(π-θ),
∵θ∈(0,
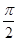 ),
),∴π-θ∈(
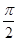 ,π),
,π),故有 α=π-θ.
故答案为D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
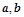 是两个互相垂直的非零向量,则在以下给出的式子“①
是两个互相垂直的非零向量,则在以下给出的式子“①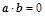 ;②
;②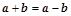 ;③
;③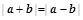 ;④
;④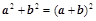 ;⑤
;⑤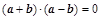 ”中正确的有【 】.
”中正确的有【 】.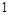 个
个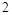 个
个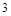 个
个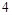 个
个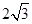 ,若OC=
,若OC=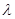 OA+
OA+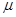 OB,
OB,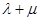 的值为 ( )
的值为 ( )
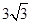 D.4
D.4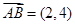 ,
,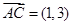 ,则
,则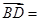 ( )
( )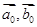 分别是与
分别是与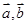 同向的单位向量,则下列结论中正确的是
同向的单位向量,则下列结论中正确的是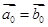 B
B 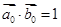
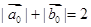 D
D 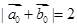
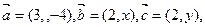 已知
已知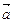 ∥
∥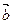 ,
,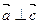 ,
,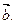 和向量
和向量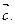 (2)求
(2)求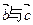 夹角。
夹角。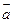 ,
,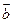 为两个相互垂直的单位向量.已知
为两个相互垂直的单位向量.已知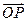 =
=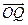 =
=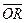 =r
=r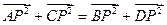 ,则四边形ABCD是( )
,则四边形ABCD是( )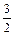 ,sinα),b=(cosα,
,sinα),b=(cosα,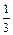 ),且a// b,则锐角α为 ___________________
),且a// b,则锐角α为 ___________________