题目内容
在△ABC中,tanA= ,tanB=
,tanB=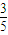 .
.(I)求角C的大小;
(II)若AB边的长为
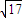 ,求BC边的长.
,求BC边的长.
【答案】分析:(I)利用三角形内角和可知tanC=-tan(A+B)然后利用正切的两角和公式求得tan(A+B)的值,进而求得tanC的值,则C的值可求.
(II)利用tanA的值求得sinA和cosA的关系式,进而利用二者的平方关系联立求得sinA,最后利用正弦定理求得BC的值.
解答:解:(I)∵C=π-(A+B),
∴tanC=-tan(A+B)=-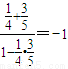 ,
,
又∵0<C<π,
∴C=
(II)由 且A∈(0,
且A∈(0,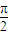 ),
),
得sinA= .
.
∵ ,
,
∴BC=AB• .
.
点评:本小题主要考查两角和差公式,用同角三角函数关系等解斜三角形的基本知识以及推理知运算能力.
(II)利用tanA的值求得sinA和cosA的关系式,进而利用二者的平方关系联立求得sinA,最后利用正弦定理求得BC的值.
解答:解:(I)∵C=π-(A+B),
∴tanC=-tan(A+B)=-
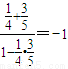 ,
,又∵0<C<π,
∴C=

(II)由
 且A∈(0,
且A∈(0,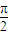 ),
),得sinA=
 .
.∵
 ,
,∴BC=AB•
 .
.点评:本小题主要考查两角和差公式,用同角三角函数关系等解斜三角形的基本知识以及推理知运算能力.

练习册系列答案
相关题目


 =2sinC。
=2sinC。