题目内容
吉安市某校高二年级抽取了20名学生的今年三月、四月、五月三个月的月考的数学、化学成绩,计算了他们三次成绩的平均分如下表:| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数学 | 120 | 105 | 91 | 124 | 85 | 132 | 121 | 100 | 78 | 135 |
| 化学 | 70 | 68 | 74 | 82 | 78 | 71 | 81 | 62 | 54 | 90 |
| 学生序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 数学 | 132 | 92 | 85 | 123 | 100 | 97 | 101 | 96 | 103 | 105 |
| 化学 | 85 | 65 | 53 | 77 | 63 | 85 | 73 | 45 | 84 | 72 |
(1)从这20名学生中随机抽取2名,用X表示数学成绩优秀的人数,求X的分布列及数学期望;
(2)根据这次抽查数据,是否在犯错误的概率不超过10%的前提下认为化学成绩优秀与否和数学成绩优秀与否有关?
【答案】分析:(1)确定X的可能取值,求出相应的概率,即可得到分布列,从而求出数学期望;
(2)写出列联表,求出X2,与临界值比较,即可得到结论.
解答:解:(1)由已知可得:数学成绩优秀的人数为7,数学成绩不优秀的人数为13,
则X可能取的值为0,1,2;(1分)
且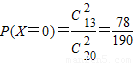 ,
,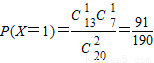 ,
,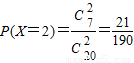 (4分)
(4分)
则X的分布列为
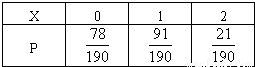
且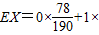
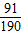 +
+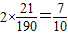 (6分)
(6分)
(2)由已知可得:这名学生数学优秀及不优秀,化学优秀及不优秀的人数如下表
(8分)
则: (10分)
(10分)
则:可以认为在犯错误的概率不超过10%的前提下化学成绩优秀和数学成绩优秀有关.(12分)
点评:本题考查概率的计算,考查独立性检验知识的运用,考查学生分析解决问题的能力,属于中档题.
(2)写出列联表,求出X2,与临界值比较,即可得到结论.
解答:解:(1)由已知可得:数学成绩优秀的人数为7,数学成绩不优秀的人数为13,
则X可能取的值为0,1,2;(1分)
且
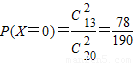 ,
,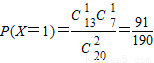 ,
,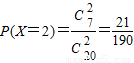 (4分)
(4分)则X的分布列为

且
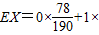
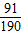 +
+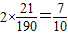 (6分)
(6分)(2)由已知可得:这名学生数学优秀及不优秀,化学优秀及不优秀的人数如下表
| 数学优秀 | 数学不优秀 | 合计 | |
| 化学优秀 | 4 | 2 | 6 |
| 化学不优秀 | 3 | 11 | 14 |
| 合计 | 7 | 13 | 20 |
则:
 (10分)
(10分)则:可以认为在犯错误的概率不超过10%的前提下化学成绩优秀和数学成绩优秀有关.(12分)
点评:本题考查概率的计算,考查独立性检验知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目

