题目内容
已知F为抛物线C:y2=4x焦点,其准线交x轴于点M,点N是抛物线C上一点(Ⅰ)如图1,若MN的中垂线恰好过焦点F,求点N的y轴的距离
(Ⅱ)如图2,已知直线l交抛物线C于点P,Q,若在抛物线C上存在点R,使FPRQ为平行四边形,试探究直线l是否过定点?并说明理由.
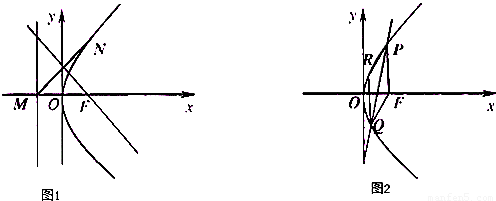
【答案】分析:(I)由中垂线的性质可得|NF|=|MF|=2,利用抛物线的定义可得xN+1=2,得到xN=1.即可求出点N到y轴的距离.
(II)设P(x1,y1),Q(x2,y2),直线l:x=my+b.由FPRQ为平行四边形,可得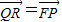 .利用向量相等即可得出坐标之间的关系,再将直线l的方程与抛物线的方程联立得到根与系数的关系,从而得出定点.
.利用向量相等即可得出坐标之间的关系,再将直线l的方程与抛物线的方程联立得到根与系数的关系,从而得出定点.
解答:解:(I)∵MN的中垂线恰好经过焦点F,∴|NF|=|MF|=2,
∴xN+1=2,
∴xN=1.即点N到y轴的距离为1.
(II)焦点F(1,0),
设P(x1,y1),Q(x2,y2),直线l:x=my+b.
∵FPRQ为平行四边形,∴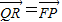 .
.
∴x1+x2=xR+1,y1+y2=yR.
∵点R在抛物线上,∴ ,即
,即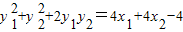 .
.
又点P,Q在抛物线上,∴y1y2=-2.由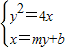 得y2-4my-4b=0,∴y1y2=-4b.∴-4b=-2,解得
得y2-4my-4b=0,∴y1y2=-4b.∴-4b=-2,解得 .
.
∴直线l经过定点
点评:熟练掌握抛物线的定义、线段垂直平分线的性质、向量相等、直线与抛物线相交问题转化为方程联立得到根与系数的关系是解题的关键.
(II)设P(x1,y1),Q(x2,y2),直线l:x=my+b.由FPRQ为平行四边形,可得
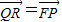 .利用向量相等即可得出坐标之间的关系,再将直线l的方程与抛物线的方程联立得到根与系数的关系,从而得出定点.
.利用向量相等即可得出坐标之间的关系,再将直线l的方程与抛物线的方程联立得到根与系数的关系,从而得出定点.解答:解:(I)∵MN的中垂线恰好经过焦点F,∴|NF|=|MF|=2,
∴xN+1=2,
∴xN=1.即点N到y轴的距离为1.
(II)焦点F(1,0),
设P(x1,y1),Q(x2,y2),直线l:x=my+b.
∵FPRQ为平行四边形,∴
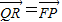 .
.∴x1+x2=xR+1,y1+y2=yR.
∵点R在抛物线上,∴
 ,即
,即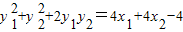 .
.又点P,Q在抛物线上,∴y1y2=-2.由
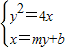 得y2-4my-4b=0,∴y1y2=-4b.∴-4b=-2,解得
得y2-4my-4b=0,∴y1y2=-4b.∴-4b=-2,解得 .
.∴直线l经过定点

点评:熟练掌握抛物线的定义、线段垂直平分线的性质、向量相等、直线与抛物线相交问题转化为方程联立得到根与系数的关系是解题的关键.

练习册系列答案
相关题目

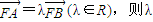 为何值时,直线AB与抛物线C所围成的图形的面积最小?该面积的最小值是多少?
为何值时,直线AB与抛物线C所围成的图形的面积最小?该面积的最小值是多少? ,求线段AB的中点M的轨迹方程.
,求线段AB的中点M的轨迹方程.