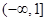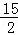题目内容
定义:若存在常数 ,使得对定义域
,使得对定义域 内的任意两个
内的任意两个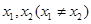 ,均有
,均有 成立,则称函数
成立,则称函数 在定义域
在定义域 上满足利普希茨条件.若函数
上满足利普希茨条件.若函数 满足利普希茨条件,则常数
满足利普希茨条件,则常数 的最小值为( )
的最小值为( )
| A.4 | B.3 | C.1 | D. |
D
解析试题分析:由已知中中利普希茨条件的定义,若函数 满足利普希茨条件,所以存在常数k,使得对定义域[1,+∞)内的任意两个
满足利普希茨条件,所以存在常数k,使得对定义域[1,+∞)内的任意两个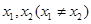 ,均有
,均有 成立, 不妨设
成立, 不妨设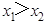 ,则
,则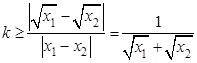 . 而0<
. 而0< <
<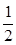 ,所以k的最小值为
,所以k的最小值为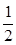 .故选D.
.故选D.
考点:1.新定义问题;2.函数恒成立问题.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
已知函数 .那么不等式
.那么不等式 的解集为( ).
的解集为( ).
A. | B. |
C. | D. |
已知 ,且
,且 ,
,
成等比数列,则xy( )
| A.有最大值e | B.有最大值 |
| C.有最小值e | D.有最小值 |
下列所给4个图象中,与所给3件事吻合最好的顺序为( )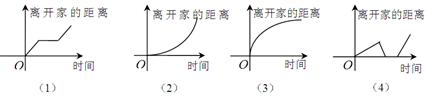
(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;
(2)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;
(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速。
| A.(1)(2)(4) | B.(4)(2)(3) | C.(4)(1)(3) | D.(4)(1)(2) |
(2014·嘉兴模拟)已知a= ,b=0.3-2,c=lo
,b=0.3-2,c=lo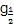 2,则a,b,c的大小关系是( )
2,则a,b,c的大小关系是( )
| A.a>b>c | B.a>c>b | C.c>b>a | D.b>a>c |
若函数f(x)的导函数是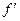 (x)=-x(x+1),则函数g(x)=f(logax)(0<a<1)的单调递减区间是( )
(x)=-x(x+1),则函数g(x)=f(logax)(0<a<1)的单调递减区间是( )
| A.[-1,0] | B.[ ,+∞),(0,1] ,+∞),(0,1] |
C.[1,  ] ] | D.(-∞, ) ,( ) ,( ,+∞) ,+∞) |
已知函数f(x)=ax-1+3(a>0且a≠1)的图象过一个定点P,且点P在直线mx+ny-1=0(m>0,且n>0)上,则 的最小值是( )
的最小值是( )
| A.12 | B.16 | C.25 | D.24 |
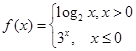 ,且函数
,且函数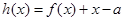 有且只有一个零点,则实数
有且只有一个零点,则实数 的取值范围是( )
的取值范围是( )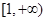 B.
B.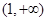
 .
.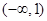 D.
D.